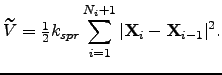 | (4.1) |
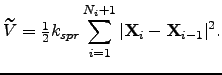 | (4.1) |
![\begin{psfrags}
\psfrag{z} [Bl][Bl]{$V\left( \bfx \right)$}
\psfrag{x} [Bl][...
...terline{\includegraphics[width=.45\textheight]{dneb/surface.eps}}
\end{psfrags}](img309.png) |
The springs are intended to hold images on the path during optimisation -- otherwise they would slide down to the endpoints, or to other intermediate minima [88]. Occasionally, depending on the quality of the initial guess, we have found that some images may converge to higher index stationary points. One could imagine the whole construction as a band or rope that is stretched across the PES, which, if optimised, is capable of closely following a curve defined in terms of successive minima, transition states, and the intervening steepest-descent paths.
In practice, the above formulation encounters difficulties connected with the coupling between the `true' and `spring' components of the potential. The magnitude of the springs' interference with the true potential is system dependent and generally gives rise to corner-cutting and sliding-down problems [27]. It is convenient to discuss these difficulties in terms of the components of the true gradient, ![]() , and spring gradient,
, and spring gradient, ![]() , parallel and perpendicular to the path. The parallel component of the gradient
, parallel and perpendicular to the path. The parallel component of the gradient ![]() at image
at image ![]() on the path is obtained by projecting out the perpendicular component
on the path is obtained by projecting out the perpendicular component ![]() using an estimate of the tangent to the path. The parallel and perpendicular components for image
using an estimate of the tangent to the path. The parallel and perpendicular components for image ![]() are:
are:
Corner-cutting has a significant effect when a path experiences high curvature. Here ![]() is large, which prevents the images from following the path closely because the spring force necessarily has a significant component perpendicular to the tangent. The sliding-down problem occurs due to the presence of
is large, which prevents the images from following the path closely because the spring force necessarily has a significant component perpendicular to the tangent. The sliding-down problem occurs due to the presence of ![]() , which perturbs the distribution of images along the path, creating high-resolution regions (around the local minima) and low-resolution regions (near the transition states) [27]. Both problems significantly affect the ability of the NEB method to produce good transition state candidates. We have found that sliding-down and corner-cutting are interdependent and cannot both be remedied by adjusting the spring force constant
, which perturbs the distribution of images along the path, creating high-resolution regions (around the local minima) and low-resolution regions (near the transition states) [27]. Both problems significantly affect the ability of the NEB method to produce good transition state candidates. We have found that sliding-down and corner-cutting are interdependent and cannot both be remedied by adjusting the spring force constant ![]() ;increasing
;increasing ![]() may prevent sliding-down but it will make corner-cutting worse.
may prevent sliding-down but it will make corner-cutting worse.
The aforementioned problems can sometimes be eliminated by constructing the NEB gradient from the potential in the following way: ![]() and
and ![]() are projected out, which gives the elastic band its `nudged' property [28]. Removal of
are projected out, which gives the elastic band its `nudged' property [28]. Removal of ![]() can be thought of as bringing the path into a plane or flattening the PES [Figure 2.1 (b)], while removal of
can be thought of as bringing the path into a plane or flattening the PES [Figure 2.1 (b)], while removal of ![]() is analogous to making the images heavier so that they favour the bottom of the valley at all times.
is analogous to making the images heavier so that they favour the bottom of the valley at all times.
The choice of a method to estimate the tangent to the path is important for it affects the convergence of the NEB calculation. Originally, the tangent vector, ![]() , for image
, for image ![]() was obtained by normalising the line segment between the two adjacent images,
was obtained by normalising the line segment between the two adjacent images, ![]() and
and ![]() [27]:
[27]:
![\begin{psfrags}
\psfrag{tau} [Bl][Bl]{$\bft $}
\psfrag{tab} [Bl][Bl]{$\vert ...
...centerline{\includegraphics[width=.55\textheight]{dneb/tech.eps}}
\end{psfrags}](img323.png) |
Both the above ratio, the image density and ![]() can vary depending on the system of interest, the particular pathway and other parameters of the NEB calculation. From Equation 2.3 it can be seen that
can vary depending on the system of interest, the particular pathway and other parameters of the NEB calculation. From Equation 2.3 it can be seen that ![]() , and, hence, the next step in the optimisation of image
, and, hence, the next step in the optimisation of image ![]() , is determined by its neighbours, which are not necessarily closer to the path than image
, is determined by its neighbours, which are not necessarily closer to the path than image ![]() . Therefore, a better approach in estimating the
. Therefore, a better approach in estimating the ![]() would be to use only one neighbour, since then we only need this neighbour to be better converged than image
would be to use only one neighbour, since then we only need this neighbour to be better converged than image ![]() .
.
There are two neighbours to select from, and it is natural to use the higher-energy one for this purpose, since steepest-descent paths are easier to follow downhill than uphill:
The above tangent formulation requires special handling of extrema along the path, and a mechanism for switching ![]() at such points was proposed [29]. It also fails to produce an even distribution of images in regions with high curvature [Figure 2.2 (c)]. We presume that Henkelman and Jónsson substitute
at such points was proposed [29]. It also fails to produce an even distribution of images in regions with high curvature [Figure 2.2 (c)]. We presume that Henkelman and Jónsson substitute ![]() by
by ![]() in Equation 2.2 to obtain a spring gradient formulation that will keep the images equispaced when the tangent from Equation 2.4 is used in the projections [28]:
in Equation 2.2 to obtain a spring gradient formulation that will keep the images equispaced when the tangent from Equation 2.4 is used in the projections [28]: