Next: Quenched Velocity Verlet Minimiser Up: FINDING REARRANGEMENT PATHWAYS Previous: A Double-ended Method: Nudged Contents

Optimisation of the Nudged Elastic Band

In the present work the NEB approach has been used in combination with two minimisers, namely the quenched velocity Verlet (QVV) and the limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithms. It is noteworthy that the objective function corresponding to the projected NEB gradient is unknown, but it is not actually required in either of the minimisation algorithms that we consider.

Optimisation is a general term that refers to finding stationary points of a function. Many problems in computational chemistry can be formulated as optimisation of a multidimensional function, NEB optimisation being one of the many. The goal of an optimisation problem can be formulated as follows: find a combination of parameters (independent variables) that optimise a given quantity (the objective function), possibly with some restrictions on the allowed parameter ranges [131]. To know exactly what we are looking for optimality conditions need to be defined. The condition

$\displaystyle f({\bf x}^*) < f({\bf y}) \hspace{10 mm} \forall {\bf y} \in \mho \left({\bf x}\right), {\bf y} \ne {\bf x}^*,$

(4.6)

where $\mho \left({\bf x}\right)$ is the set of all possible values of the control variable ${\bf x} = \left(x_1,x_2,...x_n \right)^T$ ,defines the global optimum ${\bf x}^*$ of the function $f({\bf x})$ .For an unconstrained problem $\mho \left({\bf x}\right)$ is infinitely large, and finding the corresponding global minimum may be a difficult task. Similarly, a point ${\bf x}^*$ is a strong local minimum of $f({\bf x})$ if

$\displaystyle f({\bf x}^*) < f({\bf y}) \hspace{10 mm} \forall {\bf y} \in \Upsilon \left({\bf x}^*,\varepsilon\right), {\bf y} \ne {\bf x}^*,$

(4.7)

where $\Upsilon \left({\bf x}^*,\varepsilon \right)$ is a set of feasible points contained in the neighbourhood $\varepsilon$ of ${\bf x}^*$ . For a weak local minimum only an inequality $f({\bf x}^*) \leqslant f({\bf y})$ must be satisfied in Equation 2.7.

More easily identified optimality conditions could be used instead of Equation 2.6 and Equation 2.7 if $f({\bf x})$ is a function with continuous first and second derivatives, namely, the stationary point and the strong local minimum conditions. A stationary point is a point where the gradient vanishes:

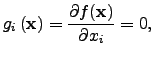$\displaystyle g_i \left( {\bf x} \right) = \frac{\partial f({\bf x})}{\partial x_i} = 0,$

(4.8)

and a strong local minimum is a stationary point where the Hessian matrix

$\displaystyle \left[{\bf H}\left({\bf x}\right)\right]_{ij} = \frac{\partial^2 f\left({\bf x}\right)}{\partial x_i \partial x_j}$

(4.9)

is positive-definite:

$\displaystyle {\bf z}^T {\bf H}\left({\bf x}\right) {\bf z} > 0 \hspace{10 mm} \forall {\bf z} \ne {\bf0}.$

(4.10)

Formally, optimisation of an NEB qualifies as a nonlinear unconstrained continuous multivariable optimisation problem. There are many algorithms available for solving problems of this type that differ in their computational requirements, convergence and other properties. However, NEB optimisation is augmented with an additional difficulty: due to the projections involved the objective function that is being minimised is unknown. Nevertheless, several optimisation techniques were found to be stable in working with NEB. Most of these are based on steepest-descent methods and, consequently, are not very efficient. The L-BFGS and QVV minimisers discussed in this section are based on the deterministic approach for finding local minima.

The basic structure of any local minimiser can be summarised as follows:

guess initial geometry ${\bf x}_0$ ;
for = 1,2,... until convergence criterion is satisfied:
1. test if convergence is achieved for current geometry ${\bf x}_i$
2. construct the search direction $\hat{\bf p}_i$
3. determine the step length $\varpi_i$
4. update the geometry to ${\bf x}_i + \varpi_i \hat{\bf p}_i$

The descent direction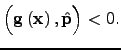 $\hat{\bf p}$ is defined as the one along which the directional derivative is negative:

$\displaystyle \Bigl(\gt \left( {\bf x} \right) , \hat{\bf p} \Bigr) < 0.$

(4.11)

Negativity of the left hand side guarantees that a lower function value will be found along $\hat{\bf p}$ provided that the step is sufficiently small. According to the way algorithms choose the search direction they are classified as non-derivative, gradient and second-derivative. Steepest-descent is an example of a gradient-based method, while BFGS belongs to the class of quasi-Newton methods (or quasi-second-derivative methods). The steepest-descent search direction is defined as the direction antiparallel to the gradient at the current point

$\displaystyle \hat{\bf p} = - \hat{\bf g},$

(4.12)

whereas second-derivative-based methods determine the search direction using the Newton-Raphson equation [31]:

$\displaystyle {\bf p} = - \hess ^{-1} {\bf g}.$

(4.13)

The step length $\varpi$ can be determined using either `line search' or `trust radius' approaches. Line search is essentially a one-dimensional minimisation of the function $\tilde{f}(\varpi) = f({\bf x}_i + \varpi {\bf p}_i)$ , which is performed at every step [131]. In the trust-radius-based approach the step length is adjusted dynamically depending on how well the minimisation algorithm predicts the change in the object function value [9]. There is no clear evidence for the superiority of one method over the other [131]; however, in combination with the limited-memory version of BFGS algorithm the trust ratio approach was found to be more efficient for treating problems with discontinuities such as problems involving periodic boundary conditions with cutoffs [9].

Subsections

Next: Quenched Velocity Verlet Minimiser Up: FINDING REARRANGEMENT PATHWAYS Previous: A Double-ended Method: Nudged Contents

Semen A Trygubenko 2006-04-10