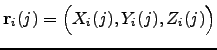 , where
, where The outcome of a pathway calculation for an atomic system will generally be a set of intermediate geometries, and the corresponding energies, for points along the two unique steepest-descent paths that link a transition state to two local minima. This discrete representation is a convenient starting point for our analysis of localisation and cooperativity. We number the structures along the path ![]() starting from one of the two minima and reversing the other steepest-descent path, so that structure
starting from one of the two minima and reversing the other steepest-descent path, so that structure ![]() corresponds to the other minimum. The transition state then lies somewhere between frames
corresponds to the other minimum. The transition state then lies somewhere between frames ![]() and
and ![]() . We define the three-dimensional vector
. We define the three-dimensional vector ![]() to contain the Cartesian coordinates of atom
to contain the Cartesian coordinates of atom ![]() for structure
for structure ![]() , i.e.
, i.e. 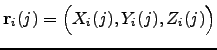 , where
, where ![]() is the
is the ![]() coordinate of atom
coordinate of atom ![]() in structure
in structure ![]() , etc.
, etc.
For each atom ![]() we also define the displacement between structures
we also define the displacement between structures ![]() and
and ![]() as
as
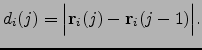 | (5.1) |
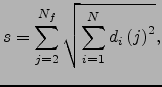 | (5.3) |
The set ![]() containing all
containing all ![]() values of
values of ![]() will be denoted
will be denoted ![]() , and analogous notation will be used for other sets below. We will also refer to the frequency distribution function, which can provide an alternative representation of such data [179]. For example, the frequency distribution function
, and analogous notation will be used for other sets below. We will also refer to the frequency distribution function, which can provide an alternative representation of such data [179]. For example, the frequency distribution function ![]() for a given continuous variable,
for a given continuous variable, ![]() , tells us that
, tells us that ![]() occurs in a certain interval
occurs in a certain interval ![]() times.
times.
Our objective in the present analysis is to provide a more detailed description of the degree of `localisation' and `cooperativity' corresponding to a given pathway. The first index we consider is ![]() , which is designed to provide an estimate of how many atoms participate in the rearrangement. We will refer to a rearrangement as localised if a small fraction of the atoms participate in the rearrangement, and as delocalised in the opposite limit. The second index we define,
, which is designed to provide an estimate of how many atoms participate in the rearrangement. We will refer to a rearrangement as localised if a small fraction of the atoms participate in the rearrangement, and as delocalised in the opposite limit. The second index we define, ![]() ,is intended to characterise the number of atoms that move simultaneously, i.e. cooperatively. We will refer to a rearrangement as cooperative if most of the atoms that participate in the rearrangement move simultaneously, and as uncooperative otherwise.
,is intended to characterise the number of atoms that move simultaneously, i.e. cooperatively. We will refer to a rearrangement as cooperative if most of the atoms that participate in the rearrangement move simultaneously, and as uncooperative otherwise.
The ![]() th moment about the mean for a data set
th moment about the mean for a data set ![]() is the expectation value of
is the expectation value of ![]() , where
, where ![]() and
and ![]() is the number of elements in the set. Hence for the set
is the number of elements in the set. Hence for the set ![]() defined above we define the moments,
defined above we define the moments, ![]() , as
, as
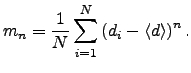 | (5.4) |
| (5.5) |
![\begin{psfrags}
\psfrag{f} [bc][bc]{$\mF _1, \mF _2$}
\psfrag{f1} [bc][bc]{$...
...rline{\includegraphics[width=.46\textheight]{coop/frequency.eps}}
\end{psfrags}](img543.png) |
The above results show that the kurtosis ![]() can be used to quantify the degree of localisation or delocalisation of a given rearrangement. However, it has the serious disadvantage that highly localised and delocalised mechanisms both have large values of
can be used to quantify the degree of localisation or delocalisation of a given rearrangement. However, it has the serious disadvantage that highly localised and delocalised mechanisms both have large values of ![]() . Since we are interested in estimating the number of atoms that move relative to the number with small or zero displacements, a better approach is to use moments taken about the origin, rather than about the mean, i.e.
. Since we are interested in estimating the number of atoms that move relative to the number with small or zero displacements, a better approach is to use moments taken about the origin, rather than about the mean, i.e.
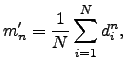 | (5.6) |
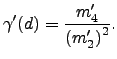 | (5.8) |
A similar index to ![]() has been employed in previous work [9,180,19] using only the displacements between the two local minima, which corresponds to taking
has been employed in previous work [9,180,19] using only the displacements between the two local minima, which corresponds to taking ![]() in Equation 3.2. Using
in Equation 3.2. Using ![]() values based upon a sum of displacements that approximates the integrated path length for atom
values based upon a sum of displacements that approximates the integrated path length for atom ![]() , rather than the overall displacement between the two minima, better reflects the character of the rearrangement, as it can account for the nonlinearity of the pathway. To describe this property more precisely we introduce a pathway nonlinearity index defined by
, rather than the overall displacement between the two minima, better reflects the character of the rearrangement, as it can account for the nonlinearity of the pathway. To describe this property more precisely we introduce a pathway nonlinearity index defined by
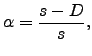 | (5.9) |
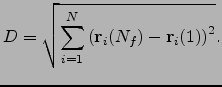 | (5.10) |
We calculated the ![]() values for a database of 31,342 single transition state pathways of LJ
values for a database of 31,342 single transition state pathways of LJ![]() (hereafter referred to as the LJ
(hereafter referred to as the LJ![]() database). The average value of
database). The average value of ![]() was
was ![]() with a standard deviation of
with a standard deviation of ![]() , and, hence, there is a significant loss of information if
, and, hence, there is a significant loss of information if ![]() is calculated only from the endpoints using
is calculated only from the endpoints using ![]() . Comparison of the two indices for the LJ
. Comparison of the two indices for the LJ![]() database revealed many examples where neglect of intermediate structures produces a misleading impression of the number of atoms that move. The definition in Equation 3.7 is therefore suggested as an improvement on previous indices of localisation [9,152,180,19].
database revealed many examples where neglect of intermediate structures produces a misleading impression of the number of atoms that move. The definition in Equation 3.7 is therefore suggested as an improvement on previous indices of localisation [9,152,180,19].