Mean Escape Times

Next: Chain Graphs Up: Introduction Previous: KMC and DPS Averages Contents

Mean Escape Times

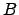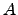Since the mean first passage time between states and , or the escape time from a subgraph, is of particular interest, we first illustrate a means to derive formulae for these quantities in terms of pathway probabilities.

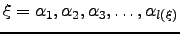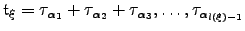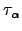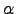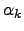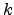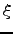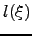The average time taken to traverse a path $\xi = \alpha_1,\alpha_2,\alpha_3,\dots,\alpha_{l(\xi)}$ is calculated as $\mathfrak{t}_{\xi} = \tau_{\alpha_1}+\tau_{\alpha_2}+\tau_{\alpha_3},\dots,\tau_{\alpha_{l(\xi)-1}}$ , where $\tau_\alpha$ is the mean waiting time for escape from node $\alpha$ , as above, $\alpha_k$ identifies the th node along path $\xi$ , and $l(\xi)$ is the length of path 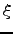$\xi$ .The mean escape time from a graph 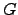if started from node 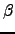$\beta$ is then

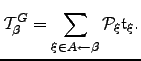$\displaystyle \mathcal{T}^{G}_\beta = \sum_{\xi \in A\leftarrow\beta} \mathcal{P}_{\xi} \mathfrak{t}_{\xi}.$

(6.20)

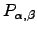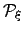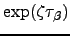If we multiply every branching probability, $P_{\alpha,\beta}$ , that appears in $\mathcal{P}_{\xi}$ by $\exp(\zeta \tau_\beta)$ then the mean escape time can be obtained as:

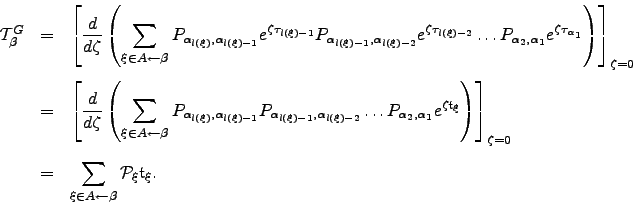$\begin{displaymath}\begin{array}{lll} \mathcal{T}^{G}_\beta &=& \displaystyle \l... ...ftarrow\beta} \mathcal{P}_{\xi} \mathfrak{t}_{\xi}. \end{array}\end{displaymath}$

(6.21)

This approach is useful if we have analytic results for the total probability 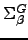$\Sigma^{G}_\beta$ , which may then be manipulated into formulae for 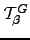$\mathcal{T}^{G}_\beta$ , and is standard practice in probability theory literature [208,209]. The quantity 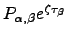$P_{\alpha,\beta}e^{\zeta\tau_\beta}$ is similar to the ` 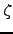$\zeta$ probability' described in Reference GoldhirschG86. Analogous techniques are usually employed to obtain 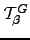$\mathcal{T}^{G}_\beta$ and higher moments of the first-passage time distribution from analytic expressions for the first-passage probability generating function (see, for example, References Raykin92,MurthyK89). We now define 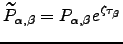$\tilde{P}_{\alpha,\beta} = P_{\alpha,\beta} e^{\zeta\tau_\beta}$ and the related quantities

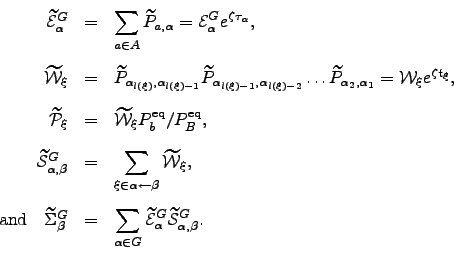$\begin{displaymath}\begin{array}{rll} \mEt _{\alpha}^{G} &=& \dsum _{a\in A} \ti... ...\in G} \mEt _{\alpha}^{G} \mSt _{\alpha,\beta}^{G}. \end{array}\end{displaymath}$

(6.22)

Note that $\left[\mEt _{\alpha}^{G}\right]_{\zeta=0} = \mE _{\alpha}^{G}$ etc., while the mean escape time can now be written as

$\displaystyle \mathcal{T}^{G}_\beta = \left[ \frac{d\tilde{\Sigma}_\beta^{G}}{d\zeta} \right]_{\zeta=0}.$

(6.23)

In the remaining sections we show how to calculate the pathway probabilities, 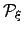$\mathcal{P}_\xi$ , exactly, along with pathway averages, such as the waiting time. Chain graphs are treated in Section 4.2 and the results are generalised to arbitrary graphs in Section 4.3.

Next: Chain Graphs Up: Introduction Previous: KMC and DPS Averages Contents

Semen A Trygubenko 2006-04-10