next up previous contents
Next: Complete Graphs Up: ENSEMBLES OF REARRANGEMENT PATHWAYS Previous: Mean Escape Times   Contents


Chain Graphs

A general account of the problem of the first passage time in chemical physics was given by Weiss as early as 1965 [212]. In Reference Weiss67 he summarised various techniques for solving such problems to date, and gave a general formula for moments of the first passage time in terms of the Green's function of the Fokker-Plank operator. Explicit expressions for the mean first passage times in terms of the basic transition probabilities for the case of a one-dimensional random walk were obtained by Ledermann and Reuter in 1954 [213], Karlin and MacGregor in 1957 [214], Weiss in 1965 [212], Gardiner in 1985 [215], Van den Broeck in 1988 [216], Le Doussal in 1989 [217], Murthy and Kehr and Matan and Havlin in 1989-1990 [219,211,218], Raykin in 1992 [210], Bar-Haim and Klafter in 1998 [203], Pury and Cáceres in 2003 [220], and Slutsky, Kardar and Mirny in 2004 [221,222]. The one-dimensional random walk is therefore a very well researched topic, both in the field of probability and its physical and chemical applications. The results presented in this section differ in the manner of presentation.

A random walk in a discrete state space $ S$, where all the states can be arranged on a linear chain in such a way that $ P_{i,j}=0$ for all $ \vert i-j\vert>1$, is called a one-dimensional or simple random walk (SRW). The SRW model attracts a lot of attention because of its rich behaviour and mathematical tractability. A well known example of its complexity is the anomalous diffusion law discovered by Sinai [223]. He showed that there is a dramatic slowing down of an ordinary power law diffusion (RMS displacement is proportional to $ (\log t)^2$ instead of $ t^{1/2}$) if a random walker at each site $ i$ experiences a random bias field $ B_i=P_{i,i+1}-P_{i,i-1}$. Stanley and Havlin generalised the Sinai model by introducing long-range correlations between the bias fields on each site and showed that the SRW can span a range of diffusive properties [224].

Although one-dimensional transport is rarely found on the macroscopic scale at a microscopic level there are several examples, such as kinesin motion along microtubules [226,225], or DNA translocation through a nanopore [228,227], so the SRW is interesting not only from a theoretical standpoint. There is a number of models that build upon the SRW that have exciting applications, examples being the SRW walk with branching and annihilation [229], and the SRW in the presence of random trappings [230]. Techniques developed for the SRW were applied to study more complex cases, such as, for example, multistage transport in liquids [231], random walks on fractals [232,233], even-visiting random walks [234], self-avoiding random walks [235], random walks on percolation clusters [237,236], and random walks on simple regular lattices [238,239] and superlattices [240].

A presentation that discusses SRW first-passage probabilities in detail sufficient for our applications is that of Raykin [210]. He considered pathway ensembles explicitly and obtained the generating functions for the occupation probabilities of any lattice site for infinite, half-infinite and finite one-dimensional lattices with the random walker starting from an arbitrary lattice site. As we discuss below, these results have a direct application to the evaluation of the DPS rate constants augmented with recrossings. We have derived equivalent expressions for the first-passage probabilities independently, considering the finite rather than the infinite case, which we discuss in terms of chain digraphs below.

We define a chain as a digraph $ C_N=(V,E)$ with $ N$ nodes and $ 2(N-1)$ edges, where $ V=\{v_1,v_2,\dots,v_N\}$ and $ E=\{e_{1,2},e_{2,1},e_{2,3},e_{3,2},\dots,e_{N-2,N-1},e_{N-1,N-2}\}$.Adjacent nodes in the numbering scheme are connected via two oppositely directed edges, and these are the only connections. A transition probability $ P_{\alpha,\beta}$ is associated with every edge $ e_{\alpha,\beta}$, as described in Section 4.1.1. An $ N$-node chain is depicted in Figure 4.2 as a subgraph of another graph.

Figure: Chain graph of length $ N$, depicted as the subgraph of a larger graph. Visible sink nodes are shaded. Double-headed arrows represent pairs of directed edges.
\begin{psfrags} \psfrag{1} [bc][bc]{$1$} \psfrag{2} [bc][bc]{$2$} \psfrag{... ...terline{\includegraphics[width=.52\textheight]{markov/chain.eps}} \end{psfrags}
The total probability of escape from the chain via node $ N$ if started from node $ 1$ is of interest because it has previously been used to associate contributions to the total rate constant from unique paths in DPS studies [9,8]. We can restrict the sampling to paths without recrossings between intermediate minima if we perform the corresponding recrossing sums explicitly [8].

We denote a pathway in $ C_N$ by the ordered sequence of node indices. The length of a pathway is the number of edges traversed. For example, the pathway $ 1,2,1,2,3,2,3$ has length $ 6$, starts at node $ 1$ and finishes at node $ 3$. The indices of the intermediate nodes $ 2,1,2,3,2$ are given in the order in which they are visited. The product of branching probabilities associated with all edges in a path was defined above as $ \mW _\xi$. For example, the product for the above pathway is $ P_{3,2}P_{2,3}P_{3,2}P_{2,1}P_{1,2}P_{2,1}$, which we can abbreviate as $ \mW _{3,2,3,2,1,2,1}$. For a chain graph $ C_N$, which is a subgraph of $ \mathcal{G}$, we also define the set of indices of nodes in $ \mathcal{G}$ that are adjacent to nodes in $ C_N$ but not members of $ C_N$ as $ Adj[C_N]$. These nodes will be considered as sinks if we are interested in escape from $ C_N$.

Analytical results for $ C_3$ are easily derived:

\begin{displaymath}\begin{array}{lll} \mathcal{S}_{1,1}^{C_3} &= \displaystyle\s... ...3} &= \dfrac{P_{3,2}}{1-\mW _{1,2,1}-\mW _{2,3,2}}. \end{array}\end{displaymath} (6.24)

These sums converge if the cardinality of the set $ Adj[C_3]$ is greater than zero. To prove this result consider a factor, $ f$, of the form

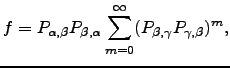$\displaystyle f = P_{\alpha,\beta}P_{\beta,\alpha} \sum_{m=0}^\infty (P_{\beta,\gamma}P_{\gamma,\beta})^m,$ (6.25)

and assume that the branching probabilities are all non-zero, and that there is at least one additional escape route from $ \alpha $, $ \beta $ or $ \gamma $. We know that $ P_{\beta,\gamma}P_{\gamma,\beta}<P_{\gamma,\beta}<1$ because $ P_{\alpha,\beta}+P_{\gamma,\beta}\leqslant1$ and $ P_{\alpha,\beta}\not=0$. Hence $ f = P_{\alpha,\beta}P_{\beta,\alpha}/(1-P_{\beta,\gamma}P_{\gamma,\beta})$. However, $ P_{\alpha,\beta}P_{\beta,\alpha}+P_{\beta,\gamma}P_{\gamma,\beta}\leqslant P_{\alpha,\beta}+P_{\gamma,\beta}\leqslant1$, and equality is only possible if $ P_{\beta,\alpha}=P_{\beta,\gamma}=P_{\alpha,\beta}+P_{\gamma,\beta}=1$, which contradicts the assumption of an additional escape route. Hence $ P_{\alpha,\beta}P_{\beta,\alpha} < 1 - P_{\beta,\gamma}P_{\gamma,\beta}$ and $ f<1$. The pathway sums $ \mathcal{S}_{1,2}^{C_3}$, $ \mathcal{S}_{1,3}^{C_3}$, $ \mathcal{S}_{2,3}^{C_3}$ and $ \mathcal{S}_{3,3}^{C_3}$ can be obtained from Equation 4.24 by permuting the indices. The last two sums in Equation 4.24 are particularly instructive: the $ n$'th term in the sum for $ \mathcal{S}_{2,2}^{C_3}$ and the $ n$'th term in the sum for $ \mathcal{S}_{3,2}^{C_3}$ are the contributions from pathways of length $ 2n$ and $ 2n+1$, respectively.

The pathway sums $ \mathcal{S}^{C_N}_{\alpha,\beta}$ can be derived for a general chain graph $ C_N$ in terms of recursion relations, as shown in Appendix C. The validity of our results for $ C_N$ was verified numerically using the matrix multiplication method described in Reference Wales02. For a chain of length $ N$ we construct an $ N\times N$ transition probability matrix $ {\bf P}$ with elements

$\displaystyle {\bf P}=\left( \begin{array}{cccc} 0 & P_{1,2} & 0 & \hdots \\ P_... ... \hdots \\ 0 & P_{3,2} & 0 & \\ \vdots & \vdots & & \ddots \end{array} \right).$ (6.26)

The matrix form of the system of Chapman-Kolmogorov equations [187] for homogeneous discrete-time Markov chains [123,187] allows us to obtain the $ n$-step transition probability matrix recursively as

$\displaystyle {\bf P}(n)={\bf P}{\bf P}(n-1)={\bf P}^{n}.$ (6.27)

$ \mathcal{S}_{\alpha,\beta}^{C_N}$ can then be computed as

$\displaystyle \mathcal{S}_{\alpha,\beta}^{C_N} = \sum_{n=1}^{M} \left[ {\bf P}^n \right]_{\alpha,\beta},$ (6.28)

where the number of matrix multiplications, $ M$, is adjusted dynamically depending on the convergence properties of the above sum. We note that sink nodes are excluded when constructing $ {\bf P}$ and $ \sum_j P_{j,i}$ can be less than unity.

For chains a sparse-optimised matrix multiplication method for $ \mathcal{S}_{\alpha,\beta}^{C_N}$ scales as $ \mathcal{O}(NM)$,and may suffer from convergence and numerical precision problems for larger values of $ N$ and branching probabilities that are close to zero or unity [8]. The summation method presented in this section can be implemented to scale as $ \mathcal{O}(N)$ with constant memory requirements (Algorithm B.1). It therefore constitutes a faster, more robust and more precise alternative to the matrix multiplication method when applied to chain graph topologies (Figure 4.3).

Figure: CPU time needed to calculate the total transition probabilities for a chain of length $ N$. The data is shown for a sparse-optimised matrix multiplication (SMM) method (blue) and a sparse-optimised version of Algorithm B.1 (red). Terminal nodes of each chain were connected to a sink, one of the terminal nodes was chosen to be the source. All the branching probabilities were set to $ 0.5$. Each SMM calculation was terminated when $ 1.0-\Sigma _{0}^{C_N}$ was less than $ 10^{-5}$. The inset shows the number of matrix multiplications, $ M$, as a function of chain length. Note the log$ _{10}$ scale on the horizontal axes.
\begin{psfrags} \psfrag{0.0} [bc][bc]{$0.0$} \psfrag{0.5} [bc][bc]{$0.5$} ... ...ine{\includegraphics[width=.47\textheight]{markov/alg1VSsmm.eps}} \end{psfrags}

Mean escape times for $ C_3$ are readily obtained from the results in Equation 4.24 by applying the method outlined in Section 4.1.5:

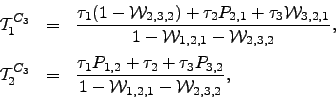\begin{displaymath}\begin{array}{lll} \mathcal{T}^{C_3}_1 &=& \dfrac{\tau_1 (1-\... ...tau_2+\tau_3 P_{3,2}}{1-\mW _{1,2,1}-\mW _{2,3,2}}, \end{array}\end{displaymath} (6.29)

and $ \mathcal{T}^{C_3}_3$ can be obtained from $ \mathcal{T}^{C_3}_1$ by permuting the subscripts 1 and 3.

The mean escape time from the $ C_N$ graph if started from node $ \beta $ can be calculated recursively using the results of Appendix D and Section 4.1.5 or by resorting to a first-step analysis [241].

next up previous contents
Next: Complete Graphs Up: ENSEMBLES OF REARRANGEMENT PATHWAYS Previous: Mean Escape Times   Contents
Semen A Trygubenko 2006-04-10