


Next: Graph Transformation Method Up: ENSEMBLES OF REARRANGEMENT PATHWAYS Previous: Chain Graphs Contents
Complete Graphs
In a complete digraph each pair of nodes is connected by two oppositely directed edges [155]. The complete graph with 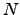 graph nodes is denoted
graph nodes is denoted 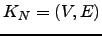 , and has
, and has 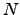 nodes and
nodes and 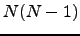 edges, remembering that we have two edges per connection (Figure 4.4).
edges, remembering that we have two edges per connection (Figure 4.4).
Figure: Complete graphs 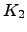 and
and 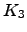 , depicted as the subgraphs of a larger graph. Visible sink nodes are shaded.
, depicted as the subgraphs of a larger graph. Visible sink nodes are shaded. ![\begin{psfrags}
\psfrag{1} [bc][bc]{$1$}
\psfrag{2} [bc][bc]{$2$}
\psfrag{...
...ncludegraphics[width=.52\textheight]{markov/complete_graphs.eps}}
\end{psfrags}](img764.png) |
Due to the complete connectivity we need only consider two cases: when the starting and finishing nodes are the same and when they are distinct. We employ complete graphs for the purposes of generality. An arbitrary graph 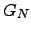 is a subgraph of
is a subgraph of 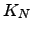 with transition probabilities for non-existent edges set to zero. All the results in this section are therefore equally applicable to arbitrary graphs.
with transition probabilities for non-existent edges set to zero. All the results in this section are therefore equally applicable to arbitrary graphs. The complete graph 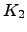 will not be considered here as it is topologically identical to the graph
will not be considered here as it is topologically identical to the graph 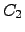 . The difference between the
. The difference between the 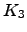 and
and 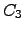 graphs is the existence of edges that connect nodes
graphs is the existence of edges that connect nodes 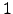 and
and 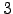 . Pathways confined to
. Pathways confined to 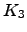 can therefore contain cycles, and for a given path length they are significantly more numerous (Figure 4.5).
can therefore contain cycles, and for a given path length they are significantly more numerous (Figure 4.5).
Figure: The growth of the number of pathways with the pathway length for 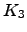 and
and 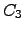 . The starting node is chosen arbitrarily for
. The starting node is chosen arbitrarily for 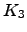 while for
while for 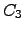 the we start at one of the terminal nodes. Any node adjacent to
the we start at one of the terminal nodes. Any node adjacent to 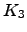 or
or 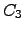 is a considered to be a sink and for simplicity we consider only one escape route from every node. Note the log
is a considered to be a sink and for simplicity we consider only one escape route from every node. Note the log scale on the vertical axis.
scale on the vertical axis. ![\begin{psfrags}
\psfrag{K3} [bc][bc]{$K_3$}
\psfrag{C3} [bc][bc]{$C_3$}
\p...
...ncludegraphics[width=.47\textheight]{markov/number_of_paths.eps}}
\end{psfrags}](img766.png) |
The 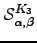 can again be derived analytically for this graph:
can again be derived analytically for this graph: 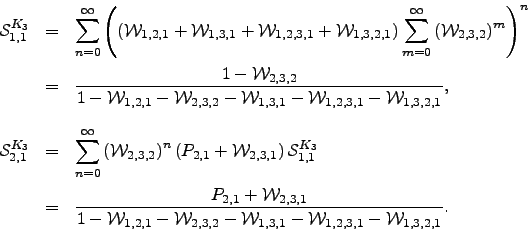 | (6.30) |
The results for any other possibility can be obtained by permuting the node indices appropriately. The pathway sums 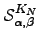 for larger complete graphs can be obtained by recursion. For
for larger complete graphs can be obtained by recursion. For 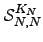 any path leaving from and returning to
any path leaving from and returning to 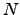 can be broken down into a step out of
can be broken down into a step out of 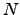 to any
to any 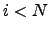 , all possible paths between
, all possible paths between 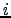 and
and 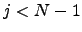 within
within 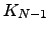 , and finally a step back to
, and finally a step back to 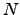 from
from 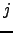 . All such paths can be combined together in any order, so we have a multinomial distribution [242]:
. All such paths can be combined together in any order, so we have a multinomial distribution [242]:
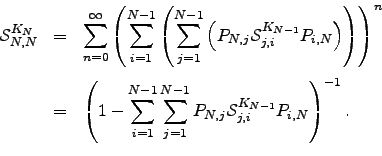 | (6.31) |
To evaluate 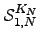 we break down the sum into all paths that depart from and return to
we break down the sum into all paths that depart from and return to 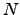 , followed by all paths that leave node
, followed by all paths that leave node 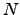 and reach node 1 without returning to
and reach node 1 without returning to 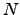 . The first contribution corresponds to a factor of
. The first contribution corresponds to a factor of 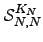 , and the second produces a factor
, and the second produces a factor 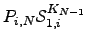 for every
for every 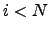 :
: 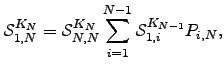 | (6.32) |
where 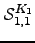 is defined to be unity. Any other
is defined to be unity. Any other 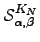 can be obtained by a permutation of node labels.
can be obtained by a permutation of node labels. Algorithm B.2 provides an example implementation of the above formulae optimised for incomplete graphs. The running time of Algorithm B.2 depends strongly on the graph density. (A digraph in which the number of edges is close to the maximum value of 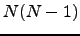 is termed a dense digraph [202].) For
is termed a dense digraph [202].) For 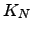 the algorithm runs in
the algorithm runs in 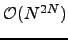 time, while for an arbitrary graph it scales as
time, while for an arbitrary graph it scales as 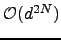 , where
, where 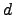 is the average degree of the nodes. For chain graphs the algorithm runs in
is the average degree of the nodes. For chain graphs the algorithm runs in 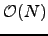 time and therefore constitutes a recursive-function-based alternative to Algorithm B.1 with linear memory requirements. For complete graphs an alternative implementation with
time and therefore constitutes a recursive-function-based alternative to Algorithm B.1 with linear memory requirements. For complete graphs an alternative implementation with 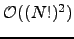 scaling is also possible.
scaling is also possible.
Although the scaling of the above algorithm with 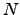 may appear disastrous, it does in fact run faster than standard KMC and MM approaches for graphs where the escape probabilities are several orders of magnitude smaller than the transition probabilities (Algorithm B.2). Otherwise, for anything but moderately branched chain graphs, Algorithm B.2 is significantly more expensive. However, the graph-transformation-based method presented in Section 4.4 yields both the pathway sums and the mean escape times for a complete graph
may appear disastrous, it does in fact run faster than standard KMC and MM approaches for graphs where the escape probabilities are several orders of magnitude smaller than the transition probabilities (Algorithm B.2). Otherwise, for anything but moderately branched chain graphs, Algorithm B.2 is significantly more expensive. However, the graph-transformation-based method presented in Section 4.4 yields both the pathway sums and the mean escape times for a complete graph 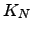 in
in 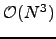 time, and is the fastest approach that we have found.
time, and is the fastest approach that we have found.
Mean escape times for 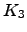 are readily obtained from the results in Equation 4.30 by applying the method outlined in Section 4.1.5:
are readily obtained from the results in Equation 4.30 by applying the method outlined in Section 4.1.5:
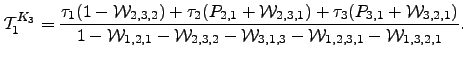 | (6.33) |
We have verified this result analytically using first-step analysis and numerically for various values of the parameters 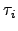 and
and 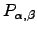 . and obtained quantitative agreement (see Figure 4.6).
. and obtained quantitative agreement (see Figure 4.6). Figure: Mean escape time from 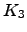 as a function of the escape probability
as a function of the escape probability 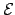 . The transition probabilities for the
. The transition probabilities for the 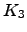 graph are parametrised by
graph are parametrised by 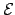 for simplicity:
for simplicity: 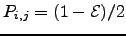 for all
for all 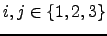 and
and 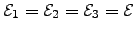 . Kinetic Monte Carlo data (triangles) was obtained by averaging over
. Kinetic Monte Carlo data (triangles) was obtained by averaging over 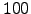 trajectories for each of 33 parameterisations. The solid line is the exact solution obtained using Equation 4.33. The units of
trajectories for each of 33 parameterisations. The solid line is the exact solution obtained using Equation 4.33. The units of 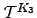 are arbitrary. Note the log
are arbitrary. Note the log scale on the vertical axis.
scale on the vertical axis. ![\begin{psfrags}
\psfrag{Tau} [bc][bc]{$\log_{10}\mathcal{T}^{K_3}$}
\psfrag{...
...ncludegraphics[width=.47\textheight]{markov/K3_waiting_time.eps}}
\end{psfrags}](img785.png) |
Figure 4.7 demonstrates how the advantage of exact summation over KMC and MM becomes more pronounced as the escape probabilities become smaller. Figure: The computational cost of the kinetic Monte Carlo and matrix multiplication methods as a function of escape probability for 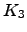 (see caption to Figure 4.6 for the definition of
(see caption to Figure 4.6 for the definition of 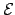 ).
). 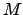 is the number of matrix multiplications required to converge the value of the total probability of getting from node
is the number of matrix multiplications required to converge the value of the total probability of getting from node 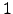 to nodes
to nodes 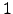 ,
, 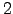 and
and 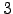 : the calculation was terminated when the change in the total probability between iterations was less than
: the calculation was terminated when the change in the total probability between iterations was less than 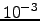 . The number of matrix multiplications
. The number of matrix multiplications 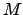 and the average trajectory length
and the average trajectory length 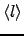 can be used as a measure of the computational cost of the matrix multiplication and kinetic Monte Carlo approaches, respectively. The computational requirements of the exact summation method are independent of
can be used as a measure of the computational cost of the matrix multiplication and kinetic Monte Carlo approaches, respectively. The computational requirements of the exact summation method are independent of 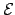 . Note the log
. Note the log scale on the vertical axis.
scale on the vertical axis. ![\begin{psfrags}
\psfrag{M} [bc][bc]{$\log_{10}M$}
\psfrag{n} [bc][bc]{$\log_...
...graphics[width=.47\textheight]{markov/K3_computational_cost.eps}}
\end{psfrags}](img790.png) |



Next: Graph Transformation Method Up: ENSEMBLES OF REARRANGEMENT PATHWAYS Previous: Chain Graphs Contents Semen A Trygubenko 2006-04-10 ![]() graph nodes is denoted
graph nodes is denoted ![]() , and has
, and has ![]() nodes and
nodes and ![]() edges, remembering that we have two edges per connection (Figure 4.4).
edges, remembering that we have two edges per connection (Figure 4.4). ![\begin{psfrags}
\psfrag{1} [bc][bc]{$1$}
\psfrag{2} [bc][bc]{$2$}
\psfrag{...
...ncludegraphics[width=.52\textheight]{markov/complete_graphs.eps}}
\end{psfrags}](img764.png)
![]() will not be considered here as it is topologically identical to the graph
will not be considered here as it is topologically identical to the graph ![]() . The difference between the
. The difference between the ![]() and
and ![]() graphs is the existence of edges that connect nodes
graphs is the existence of edges that connect nodes ![]() and
and ![]() . Pathways confined to
. Pathways confined to ![]() can therefore contain cycles, and for a given path length they are significantly more numerous (Figure 4.5).
can therefore contain cycles, and for a given path length they are significantly more numerous (Figure 4.5). ![\begin{psfrags}
\psfrag{K3} [bc][bc]{$K_3$}
\psfrag{C3} [bc][bc]{$C_3$}
\p...
...ncludegraphics[width=.47\textheight]{markov/number_of_paths.eps}}
\end{psfrags}](img766.png)
![]() for larger complete graphs can be obtained by recursion. For
for larger complete graphs can be obtained by recursion. For ![]() any path leaving from and returning to
any path leaving from and returning to ![]() can be broken down into a step out of
can be broken down into a step out of ![]() to any
to any ![]() , all possible paths between
, all possible paths between ![]() and
and ![]() within
within ![]() , and finally a step back to
, and finally a step back to ![]() from
from ![]() . All such paths can be combined together in any order, so we have a multinomial distribution [242]:
. All such paths can be combined together in any order, so we have a multinomial distribution [242]: ![]() is termed a dense digraph [202].) For
is termed a dense digraph [202].) For ![]() the algorithm runs in
the algorithm runs in ![]() time, while for an arbitrary graph it scales as
time, while for an arbitrary graph it scales as ![]() , where
, where ![]() is the average degree of the nodes. For chain graphs the algorithm runs in
is the average degree of the nodes. For chain graphs the algorithm runs in ![]() time and therefore constitutes a recursive-function-based alternative to Algorithm B.1 with linear memory requirements. For complete graphs an alternative implementation with
time and therefore constitutes a recursive-function-based alternative to Algorithm B.1 with linear memory requirements. For complete graphs an alternative implementation with ![]() scaling is also possible.
scaling is also possible. ![]() may appear disastrous, it does in fact run faster than standard KMC and MM approaches for graphs where the escape probabilities are several orders of magnitude smaller than the transition probabilities (Algorithm B.2). Otherwise, for anything but moderately branched chain graphs, Algorithm B.2 is significantly more expensive. However, the graph-transformation-based method presented in Section 4.4 yields both the pathway sums and the mean escape times for a complete graph
may appear disastrous, it does in fact run faster than standard KMC and MM approaches for graphs where the escape probabilities are several orders of magnitude smaller than the transition probabilities (Algorithm B.2). Otherwise, for anything but moderately branched chain graphs, Algorithm B.2 is significantly more expensive. However, the graph-transformation-based method presented in Section 4.4 yields both the pathway sums and the mean escape times for a complete graph ![]() in
in ![]() time, and is the fastest approach that we have found.
time, and is the fastest approach that we have found. ![]() are readily obtained from the results in Equation 4.30 by applying the method outlined in Section 4.1.5:
are readily obtained from the results in Equation 4.30 by applying the method outlined in Section 4.1.5: ![\begin{psfrags}
\psfrag{Tau} [bc][bc]{$\log_{10}\mathcal{T}^{K_3}$}
\psfrag{...
...ncludegraphics[width=.47\textheight]{markov/K3_waiting_time.eps}}
\end{psfrags}](img785.png)
![\begin{psfrags}
\psfrag{M} [bc][bc]{$\log_{10}M$}
\psfrag{n} [bc][bc]{$\log_...
...graphics[width=.47\textheight]{markov/K3_computational_cost.eps}}
\end{psfrags}](img790.png)