next up previous contents
Next: Applications to Sparse Random Up: ENSEMBLES OF REARRANGEMENT PATHWAYS Previous: Complete Graphs   Contents


Graph Transformation Method

The problem of calculation of the properties of a random walk on irregular networks was addressed previously by Goldhirsch and Gefen [208,209]. They described a generating-function-based method where an ensemble of pathways is partitioned into `basic walks'. A walk was defined as a set of paths that satisfies a certain restriction. As the probability generating functions corresponding to these basic walks multiply, the properties of a network as a whole can be inferred given knowledge of the generating functions corresponding to these basic walks. The method was applied to a chain, a loopless regularly branched chain and a chain containing a single loop. To the best of our knowledge only one [243] out of the 30 papers [253,245,247,221,257,255,244,249,210,254,243,258,240,260,264,209,262,220,251,211,252,261,259,222,263,219,248,250,256,246] that cite the work of Goldhirsch and Gefen [208] is an application, perhaps due to the complexity of the method.

Here we present a graph transformation (GT) approach for calculating the pathway sums and the mean escape times for $ K_N$. In general, it is applicable to arbitrary digraphs, but the best performance is achieved when the graph in question is dense. The algorithm discussed in this section will be referred to as DGT (D for dense). A sparse-optimised version of the GT method (SGT) will be discussed in Section 4.5.

The GT approach is similar in spirit to the ideas that lie behind the mean value analysis and aggregation/disaggregation techniques commonly used in the performance and reliability evaluation of queueing networks [187,265,267,266]. It is also loosely related to dynamic graph algorithms [270,271,269,268], which are used when a property is calculated on a graph subject to dynamic changes, such as deletions and insertions of nodes and edges. The main idea is to progressively remove nodes from a graph whilst leaving the average properties of interest unchanged. For example, suppose we wish to remove node $ x$ from graph $ G$ to obtain a new graph $ G'$. Here we assume that $ x$ is neither source nor sink. Before node $ x$ can be removed the property of interest is averaged over all the pathways that include the edges between nodes $ x$ and $ i \in Adj[x]$.The averaging is performed separately for every node $ i$. Next, we will use the waiting time as an example of such a property and show that the mean first passage time in the original and transformed graphs is the same.

The theory is an extension of the results used to perform jumps to second neighbours in previous KMC simulations [272,8]. Consider KMC trajectories that arrive at node $ i$, which is adjacent to $ x$. We wish to step directly from $ i$ to any node in the set of nodes $ \Gamma$ that are adjacent to $ i$ or $ x$, excluding these two nodes themselves. To ensure that the mean first-passage times from sources to sinks calculated in $ G$ and $ G'$ are the same we must define new branching probabilities, $ P_{\gamma,i}'$ from $ i$ to all $ \gamma\in\Gamma$, along with a new waiting time for escape from $ i$, $ \tau_i'$. Here, $ \tau_i'$ corresponds to the mean waiting time for escape from $ i$ to any $ \gamma\in\Gamma$, while the modified branching probabilities subsume all the possible recrossings involving node $ x$ that could occur in $ G$ before a transition to a node in $ \Gamma$. Hence the new branching probabilities are:

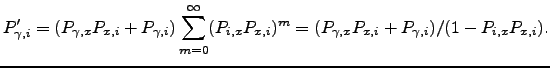$\displaystyle P_{\gamma,i}' = (P_{\gamma,x}P_{x,i}+P_{\gamma,i}) \sum_{m=0}^\infty (P_{i,x}P_{x,i})^m = (P_{\gamma,x}P_{x,i}+P_{\gamma,i})/(1-P_{i,x}P_{x,i}).$ (6.34)

This formula can also be applied if either $ P_{\gamma,i}$ or $ P_{\gamma,x}$ vanishes.

It is easy to show that the new branching probabilities are normalised:

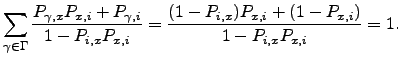$\displaystyle \sum_{\gamma\in\Gamma} \frac{P_{\gamma,x}P_{x,i}+P_{\gamma,i}}{1-P_{i,x}P_{x,i}} = \frac{(1-P_{i,x})P_{x,i}+(1-P_{x,i})}{1-P_{i,x}P_{x,i}} = 1.$ (6.35)

To calculate $ \tau_i'$ we use the method of Section 4.1.4:

$\displaystyle \tau_i' = \left[ \frac{d}{d\zeta} \sum_{\gamma\in\Gamma}\frac{P_{... ..._x+\tau_i)}} \right]_{\zeta=0} = \frac{\tau_i+P_{x,i}\tau_x}{1-P_{i,x}P_{x,i}}.$ (6.36)

The modified branching probabilities and waiting times could be used in a KMC simulation based upon graph $ G'$. Here we continue to use the notation of Section 4.1.4, where sinks correspond to nodes $ a \in A$ and sources to nodes in $ b \in B$, and $ G$ contains all the nodes in $ \mathcal{G}$ expect for the $ A$ set, as before. Since the modified branching probabilities, $ P_{\gamma,i}'$, in $ G'$ subsume the sums over all path paths from $ i$ to $ \gamma $ that involve $ x$ we would expect the sink probability, $ \Sigma_{a,b}^G$, of a trajectory starting at $ b$ ending at sink $ a$, to be conserved. However, since each trajectory exiting from $ \gamma\in\Gamma$ acquires a time increment equal to the average value, $ \tau_i'$, the mean first-passage times to individual sinks, $ \mT _{a,b}^G$, are not conserved in $ G'$ (unless there is a single sink). Nevertheless, the overall mean first-passage time to $ A$ is conserved, i.e.  $ \sum_{a\in A}\mT _{a,b}^{G'}=\mT _{b}^{G'}=\mT _{b}^{G}$. To prove these results more formally within the framework of complete sums consider the effect of removing node $ x$ on trajectories reaching node $ i \in Adj[x]$ from a source node $ b$. The sink probability for a particular sink $ a$ is

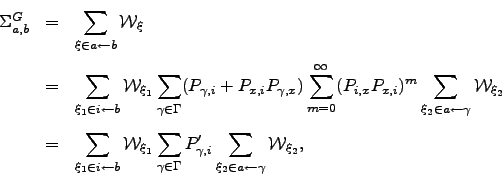\begin{displaymath}\begin{array}{lll} \Sigma_{a,b}^G &=& \displaystyle \sum_{\xi... ...i}' \sum_{\xi_2\in a\leftarrow\gamma} \mW _{\xi_2}, \end{array}\end{displaymath} (6.37)

and similarly for any other node adjacent to $ x$. Hence the transformation preserves the individual sink probabilities for any source.

Now consider the effect of removing node $ x$ on the mean first-passage time from source $ b$ to sink $ a$, $ \mT _{a,b}^{G'}$, using the approach of Section 4.1.4.

\begin{displaymath}\begin{array}{lll} \mT _{a,b}^{G'} &=& \displaystyle \left[\f... ...t[ \frac{d\mWt _{\xi_2}}{d\zeta} \right]_{\zeta=0}, \end{array}\end{displaymath} (6.38)

where the tildes indicate that every branching probability $ P_{\alpha,\beta}$ is replaced by $ P_{\alpha,\beta}e^{\xi\tau_\beta}$, as above. The first and last terms are unchanged from graph $ G$ in this construction, but the middle term,

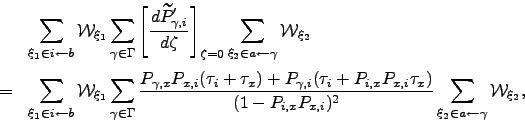\begin{displaymath}\begin{array}{lll} && \displaystyle \sum_{\xi_1 \in i\leftarr... ...^2} \sum_{\xi_2\in a\leftarrow\gamma} \mW _{\xi_2}, \end{array}\end{displaymath} (6.39)

is different (unless there is only one sink). However, if we sum over sinks then

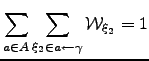$\displaystyle \sum_{a\in A}\sum_{\xi_2\in a\leftarrow\gamma} \mW _{\xi_2}=1$ (6.40)

for all $ \gamma $, and we can now simplify the sum over $ \gamma $ as

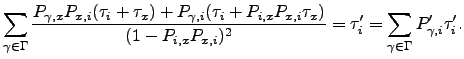$\displaystyle \sum_{\gamma\in\Gamma} \frac{P_{\gamma,x}P_{x,i}(\tau_i+\tau_x)+P... ...{(1-P_{i,x}P_{x,i})^2} = \tau_i' = \sum_{\gamma\in\Gamma} P_{\gamma,i}'\tau_i'.$ (6.41)

The same argument can be applied whenever a trajectory reaches a node adjacent to $ x$, so that $ \mT ^G_b=\mT ^{G'}_b$, as required.

The above procedure extends the BKL approach [190] to exclude not only the transitions from the current state into itself but also transitions involving an adjacent node $ x$. Alternatively, this method could be viewed as a coarse-graining of the Markov chain. Such coarse-graining is acceptable if the property of interest is the average of the distribution of times rather than the distribution of times itself. In our simulations the average is the only property of interest. In cases when the distribution itself is sought, the approach described here may still be useful and could be the first step in the analysis of the distribution of escape times, as it yields the exact average of the distribution.

The transformation is illustrated in Figure 4.8 for the case of a single source.


\begin{psfrags} \psfrag{1} [bc][bc]{$1$} \psfrag{1'} [bc][bc]{$1'$} \psfra... ...} \centerline{\includegraphics{markov/graph_transformation.eps}} \end{psfrags}
Figure: The graph transformation algorithm of Section 4.4 at work. (a) A digraph with $ 6$ nodes and $ 9$ edges. The source node is node $ 1$ (white), the sinks are nodes $ \alpha $, $ \beta $ and $ \gamma $ (shaded), and the intermediate nodes are $ 2$ and $ 3$ (black). The waiting times and transition probabilities that parametrise the graph are given below the diagram. (b) Node $ 2$ and all its incoming and outgoing edges are deleted from the graph depicted in (a). Two edges $ \beta \leftarrow 1$ and $ \beta \leftarrow 3$ are added. The parameters for this new graph are denoted by primes and expressed in terms of the parameters for the original graph. (c) Node $ 3$ is now disconnected as well. The resulting graph is composed of source and sink nodes only. The total probability and waiting times coincide with these of $ K_3$, as expected. The new parameters are denoted by a double prime.

Figure 4.8 (a) displays the original graph and its parametrisation. During the first iteration of the algorithm node $ 2$ is removed to yield the graph depicted in Figure 4.8 (b). This change reduces the dimensionality of the original graph, as the new graph contains one node and three edges fewer. The result of the second, and final, iteration of the algorithm is a graph that contains source and sink nodes only, with the correct transition probabilities and mean waiting time [Figure 4.8 (c)].

We now describe algorithms to implement the above approach and calculate mean escape times from complete graphs with multiple sources and sinks. Listings for some of the algorithms discussed here are given in Appendix B. We follow the notation of Section 4.1.4 and consider a digraph $ \mathcal{G}_N$ consisting of $ N_B$ source nodes, $ N_A$ sink nodes, and $ N_I$ intervening nodes. $ \mathcal{G}_N$ therefore contains the subgraph $ G_{N_I+N_B}$.

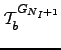The result of the transformation of a graph with a single source $ b$ and $ N_A$ sinks using Algorithm B.3 is the mean escape time $ \mathcal{T}_b^{G_{N_I+1}}$ and $ N_A$ pathway probabilities $ \mathcal{P}_{\xi}$, $ \xi\in A\leftarrow b$. Solving a problem with $ N_B$ sources is equivalent to solving $ N_B$ single source problems. 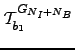For example, if there are two sources $ b_1$ and $ b_2$ we first solve a problem where only node $ b_1$ is set to be the source to obtain $ \mathcal{T}_{b_1}^{G_{N_I+N_B}}$ and the pathway sums from $ b_1$ to every sink node $ a \in A$. The same procedure is then followed for $ b_2$.

The form of the transition probability matrix $ {\bf P}$ is illustrated below at three stages: first for the original graph, then at the stage when all the intervening nodes have been removed (line 16 in Algorithm B.3), and finally at the end of the procedure:

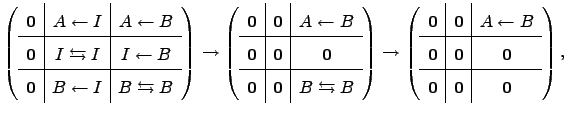$\displaystyle \left( \begin{array}{c\vert c\vert c} {\bf0} & A \leftarrow I & A... ...0} & {\bf0} & {\bf0} \\ \hline {\bf0} & {\bf0} & {\bf0} \\ \end{array} \right),$ (6.42)

Each matrix is split into blocks that specify the transitions between the nodes of a particular type, as labelled. Upon termination, every element in the top right block of matrix $ {\bf P}$ is non-zero.

Algorithm B.3 uses the adjacency matrix representation of graph $ \mathcal{G}_N$, for which the average of the distribution of mean first passage times is to be obtained. For efficiency, when constructing the transition probability matrix $ {\bf P}$ we order the nodes with the sink nodes first and the source nodes last. Algorithm B.3 is composed of two parts. The first part (lines 1-16) iteratively removes all the intermediate nodes from graph $ \mathcal{G}_N$ to yield a graph that is composed of sink nodes and source nodes only. The second part (lines 17-34) disconnects the source nodes from each other to produce a graph with $ N_A+N_B$ nodes and $ (N_A+N_B)^2$ directed edges connecting each source with every sink. Lines 13-15 are not required for obtaining the correct answer, but the final transition probability matrix looks neater.

The computational complexity of lines 1-16 of Algorithm B.3 is $ \mathcal{O}(N_I^3 + N_I^2 N_B + N_I^2 N_A + N_I N_B^2 + N_I N_B N_A)$. The second part of Algorithm B.3 (lines 17-34) scales as $ \mathcal{O}(N_B^3 + N_B^2 N_A)$. The total complexity for the case of a single source and for the case when there are no intermediate nodes is $ \mathcal{O}(N_I^3 + N_I^2 N_A)$ and $ \mathcal{O}(N_B^3 + N_B^2 N_A)$, respectively. The storage requirements of Algorithm B.3 scale as $ \mathcal{O}\left((N_I+N_B)^2\right)$.

We have implemented the algorithm in Fortran 95 and timed it for complete graphs of different sizes. The results presented in Figure 4.9 confirm the overall cubic scaling. The program is GPL-licensed [273] and available online [274]. These and other benchmarks presented in this chapter were obtained for a single Intel $ ^{\text \textregistered }$ Pentium $ ^{\text \textregistered }$ 4 3.00GHz 512Kb cache processor running under the Debian GNU/Linux operating system [275]. The code was compiled and optimised using the Intel $ ^{\text \textregistered }$ Fortran compiler for Linux.

Figure: CPU time needed to transform a dense graph $ G_{2N}$ using Algorithm B.3 as a function of $ N$. The graph $ G_{2N}$ is composed of a $ K_N$ subgraph and $ N$ sink nodes. The data is shown for six different cases, when there was a single source, and when the sources comprised 20, 40, 60, 90, and 100 percent of the number of nodes in $ K_N$, as labelled. The data for the cases $ 1$ and $ N$ was fitted as $ 5.1\times 10^{-9}N^3$ and $ 1.5\times 10^{-8}N^3$, respectively (curves not shown). For case $ 1$ only DetachNode operations were performed while for $ N$ -- only Disconnect.
\begin{psfrags} \psfrag{CPU time / s} [bc][bc]{CPU time / s} \psfrag{N} [bc]... ...r][br]{$1000$} \centerline{\includegraphics{markov/KnCPUofN.ps}} \end{psfrags}

next up previous contents
Next: Applications to Sparse Random Up: ENSEMBLES OF REARRANGEMENT PATHWAYS Previous: Complete Graphs   Contents
Semen A Trygubenko 2006-04-10