next up previous contents
Next: Internal Diffusion in LJ Up: Applications to Lennard-Jones Clusters Previous: Applications to Lennard-Jones Clusters   Contents


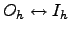$ O_h\leftrightarrow I_h$ Isomerisation of LJ$ _{38}$

We have applied the GT method to study the temperature dependence of the rate of 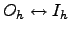$ O_h\leftrightarrow I_h$ interconversion of 38-atom Lennard-Jones cluster. The PES sample was taken from a previous study [8] and contained 1740 minima and 2072 transition states. Only geometrically distinct structures were considered when generating this sample because this way the dimensionality of the problem is reduced approximately by a factor of 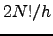$ 2N!/h$, where 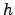$ h$ is the order of the point group. Initial and final states in this sample roughly correspond to icosahedral-like and octahedral-like structures on the PES of this cluster. The assignment was made in Reference Wales02 by solving master equation numerically to find the eigenvector that corresponds to the smallest non-zero eigenvalue. As simple two-state dynamics are associated with exponential rise and decay of occupation probabilities there must exist a time scale on which all the exponential contributions to the solution of the master equation decay to zero except for the slowest [9]. 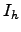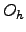The sign of the components of the eigenvector corresponding to the slowest mode was used to classify the minima as $ I_h$ or $ O_h$ in character [8].

The above sample was pruned to ensure that every minimum is reachable from any other minimum to create a digraph representation that contained 759 nodes including 43 source nodes and 5 sink nodes, and 2639 edges. The minimal, average and maximal degree for this graph were 2, 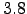$ 3.8$ and 84, respectively, and the graph density was 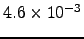$ 4.6\times10^{-3}$. We have used the SDGT algorithm with the switching ratio set to 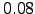$ 0.08$ to transform this graph for several values of temperature. In each of these calculations 622 out of 711 intermediate nodes were detached using SGT, and the remaining 89 intermediate nodes were detached using the GT algorithm optimised for dense graphs (DGT).

An Arrhenius plot depicting the dependence of the rate constant on temperature is shown in Figure 4.14 (a). The running time of SDGT algorithm was 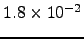$ 1.8\times10^{-2}$ seconds [this value was obtained by averaging over 10 runs and was the same for each SDGT run in Figure 4.14 (a)]. 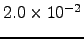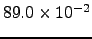For comparison, the timings obtained using the SGT and DGT algorithms for the same problem were $ 2.0\times10^{-2}$ and $ 89.0\times10^{-2}$ seconds, respectively. None of the 43 total escape probabilities (one for every source) deviated from unity by more than 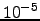$ 10^{-5}$ for temperatures above 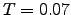$ T=0.07$ (reduced units). For lower temperatures the probability was not conserved due to numerical imprecision.

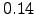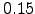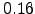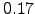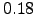The data obtained using SDGT method is compared with results from KMC simulation, which require increasingly more CPU time as the temperature is lowered. Figure 4.14 also shows the data for KMC simulations at temperatures $ 0.14$, $ 0.15$, $ 0.16$, $ 0.17$ and $ 0.18$. Each KMC simulation consisted of the generation of an ensemble of 1000 KMC trajectories from which the averages were computed. The cost of each KMC calculation is proportional to the average trajectory length, which is depicted in Figure 4.14 (b) as a function of the inverse temperature. 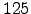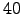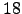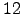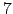The CPU timings for each of these calculations were (in the order of increasing temperature, averaged over five randomly seeded KMC simulations): $ 125$, $ 40$, $ 18$, $ 12$, and $ 7$ seconds. It can be seen that using GT method we were able to obtain kinetic data for a wider range of temperatures and with less computational expense.

Figure: (a) Arrhenius plots for the LJ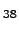$ _{38}$ cluster. 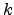$ k$ is the rate constant corresponding to transitions from icosahedral-like to octahedral-like regions. Green circles represent the data obtained from 23 SDGT runs at temperatures 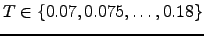$ T\in \{0.07,0.075,\dots ,0.18\}$. The data from five KMC runs is also shown (red squares). The data shown in blue corresponds to temperatures 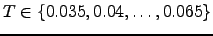$ T\in \{0.035,0.04,\dots ,0.065\}$ and was obtained using the SDGT2 method (discussed in Section 4.7.2) with quadruple precision enabled. In all SDGT runs the total escape probabilities calculated for every source at the end of the calculation deviated from unity by no more then 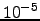$ 10^{-5}$. For this PES sample the lowest temperature for which data was reported in previous works was 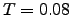$ T=0.08$. (b) The average KMC trajectory length [data in direct correspondence with KMC results shown in (a)]. A solid line is used to connect the data points to guide the eye.
\begin{psfrags} \psfrag{0} [bc][bc]{$0$} \psfrag{1} [bc][bc]{$1$} \psfrag{... ...centerline{\includegraphics{markov/arrhenius/LJ38/arrhenius.eps}} \end{psfrags}

next up previous contents
Next: Internal Diffusion in LJ Up: Applications to Lennard-Jones Clusters Previous: Applications to Lennard-Jones Clusters   Contents
Semen A Trygubenko 2006-04-10