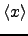 | The mean value of variable 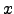 | ![[*]](crossref.png) |
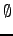 | Empty set | ![[*]](crossref.png) |
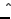 | Denotes a unit vector; 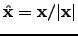 | ![[*]](crossref.png) |
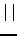 | A vector norm; 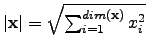 ; also, cardinality of a set ; also, cardinality of a set | ![[*]](crossref.png) |
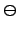 | Denotes symmetric difference of two sets | ![[*]](crossref.png) |
 | Denotes vector direct product, a.k.a. dyadic; 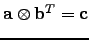 , , 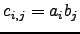 | ![[*]](crossref.png) |
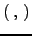 | A scalar product of two vectors, a.k.a. dot product; 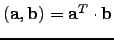 | ![[*]](crossref.png) |
 | A set of objects; 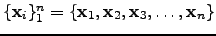 | ![[*]](crossref.png) |
 | A matrix or a vector filled with zeros | ![[*]](crossref.png) |
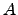 | One of the two superstates in two-state kinetic model | ![[*]](crossref.png) |
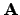 | Approximation to the inverse Hessian matrix, 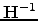 | ![[*]](crossref.png) |
![$ Adj[i]$](img195.png) | Set of all the nodes adjacent to node 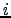 | ![[*]](crossref.png) |
![$ AdjIn[i]$](img196.png) | Set of all the nodes connected to node 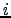 via incoming edges via incoming edges | ![[*]](crossref.png) |
![$ AdjOut[i]$](img197.png) | Set of all the nodes connected to node 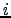 via outgoing edges via outgoing edges | ![[*]](crossref.png) |
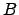 | One of the two superstates in two-state kinetic model | ![[*]](crossref.png) |
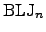 | Binary Lennard-Jones liquid with 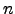 atoms in a periodic cell atoms in a periodic cell | ![[*]](crossref.png) |
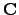 | Square matrix, columns of which are eigenvectors | ![[*]](crossref.png) |
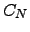 | A chain graph with 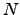 nodes nodes | ![[*]](crossref.png) |
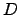 | Endpoint separation | ![[*]](crossref.png) |
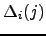 | 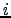 th displacement in magnitude of an atom between structures th displacement in magnitude of an atom between structures 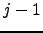 and and 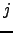 | ![[*]](crossref.png) |
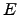 | A set of edges | ![[*]](crossref.png) |
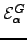 | Probability of escape from 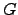 starting from starting from 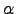 in a single step in a single step | ![[*]](crossref.png) |
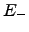 | Energy barrier corresponding to the reverse reaction | ![[*]](crossref.png) |
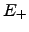 | Energy barrier corresponding to the forward reaction | ![[*]](crossref.png) |
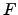 | Set of all minima connected to the final endpoint | ![[*]](crossref.png) |
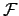 | Frequency distribution function | ![[*]](crossref.png) |
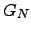 | An arbitrary graph with 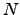 nodes nodes | ![[*]](crossref.png) |
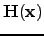 | Hessian matrix evaluated at point 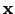 | ![[*]](crossref.png) |
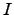 | A set containing all the minima that do not belong to 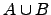 | ![[*]](crossref.png) |
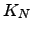 | A complete graph with 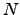 nodes nodes | ![[*]](crossref.png) |
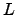 | Lagrangian function | ![[*]](crossref.png) |
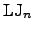 | 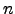 -atom Lennard-Jones cluster -atom Lennard-Jones cluster | ![[*]](crossref.png) |
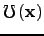 | The set of all possible values of the control variable 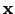 | ![[*]](crossref.png) |
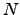 | Number of atoms; number of nodes in a graph | ![[*]](crossref.png) |
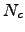 | Cooperativity index | ![[*]](crossref.png) |
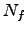 | Number of frames or points sampled along a path | ![[*]](crossref.png) |
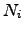 | Number of images in a band | ![[*]](crossref.png) |
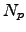 | Participation index | ![[*]](crossref.png) |
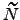 | Participation index evaluated using the endpoints alone | ![[*]](crossref.png) |
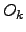 | Displacement overlap evaluated for 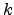 atoms using displacements atoms using displacements 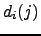 | ![[*]](crossref.png) |
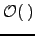 | 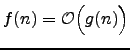 means means 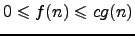 holds for some constants holds for some constants 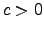 | ![[*]](crossref.png) |
 | Transition probability matrix | ![[*]](crossref.png) |
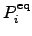 | Equilibrium occupation probability of state 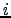 | ![[*]](crossref.png) |
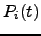 | Occupation probability of state 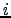 at time at time 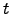 | ![[*]](crossref.png) |
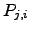 | Probability of transition from state 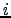 to state to state 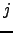 | ![[*]](crossref.png) |
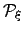 | Pathway probability | ![[*]](crossref.png) |
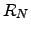 | A random graph with 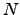 nodes nodes | ![[*]](crossref.png) |
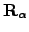 | 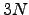 -dimensional rotation matrix about axis -dimensional rotation matrix about axis 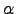 , , 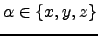 | ![[*]](crossref.png) |
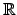 | The set of all real numbers | ![[*]](crossref.png) |
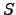 | Set of all minima connected to the starting endpoint | ![[*]](crossref.png) |
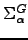 | Total probability of escape from 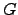 if started at node if started at node 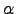 | ![[*]](crossref.png) |
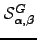 | Sum of weights of all pathways connecting 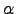 and and 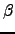 and confined to and confined to 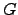 | ![[*]](crossref.png) |
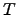 | Temperature | ![[*]](crossref.png) |
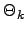 | Displacement overlap evaluated for 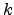 atoms using displacements atoms using displacements 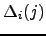 | ![[*]](crossref.png) |
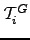 | Mean escape time from graph 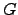 if started at node if started at node 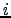 | ![[*]](crossref.png) |
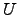 | Set of all minima that do not belong to 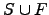 | ![[*]](crossref.png) |
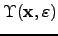 | A set of feasible points contained in the neighbourhood 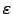 of of 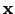 | ![[*]](crossref.png) |
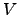 | Potential energy functional; also, a set of graph nodes | ![[*]](crossref.png) |
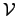 | 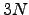 -dimensional vector of velocities[1]This vector and the other vectors defined here are column vectors. -dimensional vector of velocities[1]This vector and the other vectors defined here are column vectors. | ![[*]](crossref.png) |
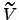 | Spring potential | ![[*]](crossref.png) |
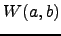 | Weight of the shortest path 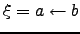 ; ; 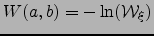 | ![[*]](crossref.png) |
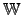 | The set of whole numbers; 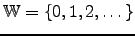 | ![[*]](crossref.png) |
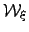 | Product of branching probabilities associated with path 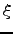 | ![[*]](crossref.png) |
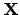 | 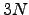 -dimensional vector representing a point in configuration space -dimensional vector representing a point in configuration space | ![[*]](crossref.png) |
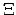 | Pathway ensemble | ![[*]](crossref.png) |
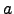 | A state that belongs to a superstate 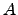 | ![[*]](crossref.png) |
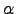 | Pathway nonlinearity index | ![[*]](crossref.png) |
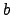 | A state that belongs to a superstate 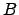 | ![[*]](crossref.png) |
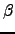 | Energy barrier asymmetry index | ![[*]](crossref.png) |
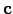 | Eigenvector | ![[*]](crossref.png) |
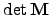 | A determinant [33] (a scalar-valued function) of matrix 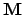 | ![[*]](crossref.png) |
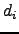 | Integrated path length for atom 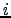 ; also, degree of node ; also, degree of node 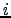 | ![[*]](crossref.png) |
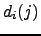 | Displacement of atom 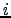 between structures between structures 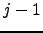 and and 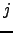 | ![[*]](crossref.png) |
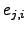 | Directed edge that describes a transition from node 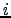 to node to node 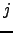 | ![[*]](crossref.png) |
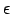 | A parameter in LJ potential (the depth of the potential energy well) | ![[*]](crossref.png) |
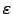 | Small positive parameter | ![[*]](crossref.png) |
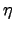 | Number of atomic degrees of freedom | ![[*]](crossref.png) |
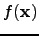 | Objective function of a vector argument 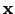 | ![[*]](crossref.png) |
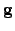 | 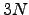 -dimensional gradient vector of the true potential -dimensional gradient vector of the true potential | ![[*]](crossref.png) |
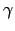 | Kurtosis of a distribution evaluated using moments about the mean | ![[*]](crossref.png) |
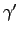 | Kurtosis of a distribution evaluated using moments about the origin | ![[*]](crossref.png) |
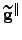 | Spring gradient vector component parallel to the path | ![[*]](crossref.png) |
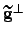 | Spring gradient vector component perpendicular to the path | ![[*]](crossref.png) |
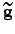 | 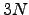 -dimensional gradient vector of the spring potential -dimensional gradient vector of the spring potential | ![[*]](crossref.png) |
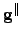 | True gradient vector component parallel to the path | ![[*]](crossref.png) |
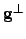 | True gradient vector component perpendicular to the path | ![[*]](crossref.png) |
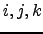 | Indices; range and meaning may vary depending on the context | ![[*]](crossref.png) |
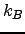 | Boltzmann's constant | ![[*]](crossref.png) |
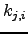 | Rate constant for transitions from state 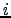 to state to state 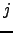 | ![[*]](crossref.png) |
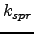 | Spring force constant | ![[*]](crossref.png) |
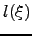 | Length of path 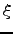 | ![[*]](crossref.png) |
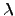 | Eigenvalue | ![[*]](crossref.png) |
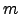 | Atomic mass | ![[*]](crossref.png) |
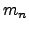 | 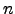 th moment of a distribution function about the mean th moment of a distribution function about the mean | ![[*]](crossref.png) |
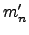 | 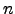 th moment of a distribution function about the origin th moment of a distribution function about the origin | ![[*]](crossref.png) |
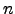 | Time parameter of a discrete-time stochastic process | ![[*]](crossref.png) |
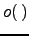 | 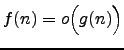 means means 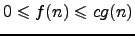 holds for all constants holds for all constants 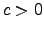 [1]Otherwise known as an upper bound that is not asymptotically tight. [1]Otherwise known as an upper bound that is not asymptotically tight. | ![[*]](crossref.png) |
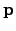 | Search direction vector | ![[*]](crossref.png) |
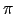 | Path length asymmetry index | ![[*]](crossref.png) |
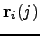 | Three-dimensional Cartesian coordinates vector of atom 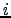 for structure for structure 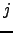 | ![[*]](crossref.png) |
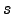 | Integrated path length | ![[*]](crossref.png) |
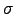 | A parameter in the LJ potential ( 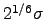 is the pair equilibrium separation) is the pair equilibrium separation) | ![[*]](crossref.png) |
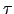 | 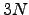 -dimensional tangent vector -dimensional tangent vector | ![[*]](crossref.png) |
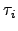 | Mean waiting time in state 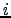 before escape before escape | ![[*]](crossref.png) |
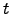 | Time | ![[*]](crossref.png) |
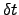 | Time integration step | ![[*]](crossref.png) |
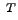 | A matrix or vector transpose | ![[*]](crossref.png) |
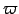 | Step size | ![[*]](crossref.png) |
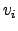 | 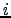 th graph node th graph node | ![[*]](crossref.png) |
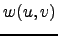 | Weight of the undirected edge connecting nodes 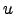 and and 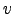 | ![[*]](crossref.png) |
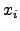 | 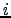 th component of vector th component of vector 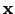 | ![[*]](crossref.png) |
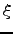 | A pathway | ![[*]](crossref.png) |
 | Vectors; dimensionality and meaning may vary depending on the context | ![[*]](crossref.png) |
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
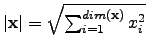 ; also, cardinality of a set
; also, cardinality of a set![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
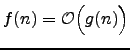 means
means ![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
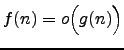 means
means ![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)

![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
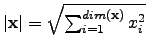 ; also, cardinality of a set
; also, cardinality of a set![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
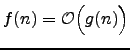 means
means ![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
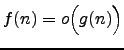 means
means ![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)