


Next: TOTAL ESCAPE PROBABILITY FOR Up: thesis Previous: ALGORITHMS Contents
PATHWAY SUMS FOR CHAIN GRAPHS, #MATH944#
To obtain the total probability of leaving the chain 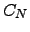 via node
via node 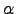 if started from node
if started from node 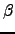 , i.e. , we must calculate the pathway sum
, i.e. , we must calculate the pathway sum 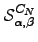 . We start with the case
. We start with the case  and obtain
and obtain 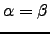 . Consider any path that has reached node
. Consider any path that has reached node 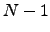 . The probability factor due to all possible
. The probability factor due to all possible 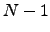 to
to 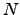 recrossings is simply
recrossings is simply 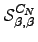 . We need to include this factor every time we reach node
. We need to include this factor every time we reach node 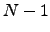 during recrossings of
during recrossings of 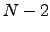 to
to 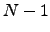 . The corresponding sum becomes
. The corresponding sum becomes 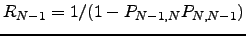 | (C.1) |
Similarly, we can continue summing contributions in this way until we have recrossings of  to
to 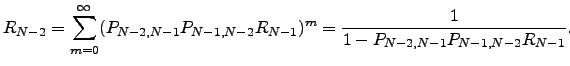 , for which the result of the nested summations is
, for which the result of the nested summations is 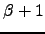 . Hence,
. Hence, 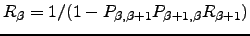 is the total transition probability for pathways that return to node
is the total transition probability for pathways that return to node 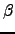 and are confined to nodes with index greater than
and are confined to nodes with index greater than 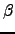 without escape from
without escape from 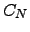 .
. We can similarly calculate the total probability for pathways returning to 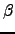 and confined to nodes with indices smaller than
and confined to nodes with indices smaller than 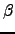 . The total probability factor for recrossings between nodes 1 and 2 is
. The total probability factor for recrossings between nodes 1 and 2 is 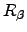 . Hence, the required probability for recrossings between nodes 2 and 3 including arbitrary recrossings between 1 and 2 is
. Hence, the required probability for recrossings between nodes 2 and 3 including arbitrary recrossings between 1 and 2 is 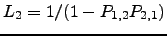 . Continuing up to recrossings between nodes
. Continuing up to recrossings between nodes 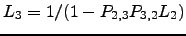 and
and 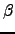 we obtain the total return probability for pathways restricted to this side of
we obtain the total return probability for pathways restricted to this side of 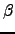 as
as 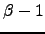 . The general recursive definitions of
. The general recursive definitions of 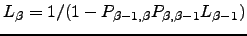 and
and 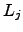 are:
are:
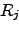 | (C.2) |
We can now calculate 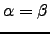 as
as
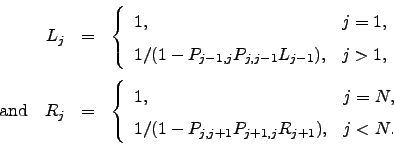 | (C.3) |
where we have used Equation C.2 and the multinomial theorem [242]. We can now derive 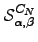 as follows. If
as follows. If 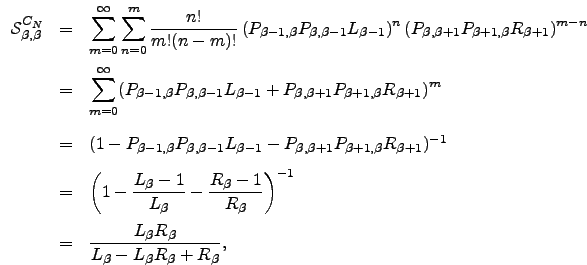 we can write
we can write
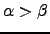 | (C.4) |
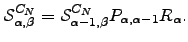 gives the total transition probability from
gives the total transition probability from 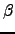 to
to 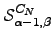 , so the corresponding probability for node
, so the corresponding probability for node 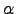 is
is 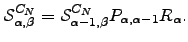 times the branching probability from
times the branching probability from 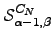 to
to 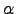 , i.e.
, i.e. 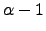 , times
, times 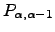 , which accounts for the weight accumulated from all possible paths that leave and return to node
, which accounts for the weight accumulated from all possible paths that leave and return to node 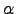 and are restricted to nodes with indexes greater than
and are restricted to nodes with indexes greater than 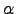 . We can now replace
. We can now replace 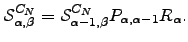 by
by 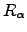 and so on, until
and so on, until 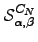 is expressed in terms of
is expressed in terms of 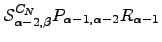 . Similarly, if
. Similarly, if 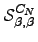 we have
we have 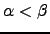 | (C.5) |
and hence 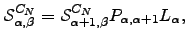 | (C.6) |

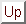


Next: TOTAL ESCAPE PROBABILITY FOR Up: thesis Previous: ALGORITHMS Contents Semen A Trygubenko 2006-04-10  and obtain
and obtain 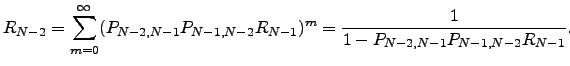 , for which the result of the nested summations is
, for which the result of the nested summations is ![]() and confined to nodes with indices smaller than
and confined to nodes with indices smaller than ![]() . The total probability factor for recrossings between nodes 1 and 2 is
. The total probability factor for recrossings between nodes 1 and 2 is ![]() . Hence, the required probability for recrossings between nodes 2 and 3 including arbitrary recrossings between 1 and 2 is
. Hence, the required probability for recrossings between nodes 2 and 3 including arbitrary recrossings between 1 and 2 is ![]() . Continuing up to recrossings between nodes
. Continuing up to recrossings between nodes ![]() and
and ![]() we obtain the total return probability for pathways restricted to this side of
we obtain the total return probability for pathways restricted to this side of ![]() as
as ![]() . The general recursive definitions of
. The general recursive definitions of ![]() and
and ![]() are:
are: ![]() as
as ![]() as follows. If
as follows. If 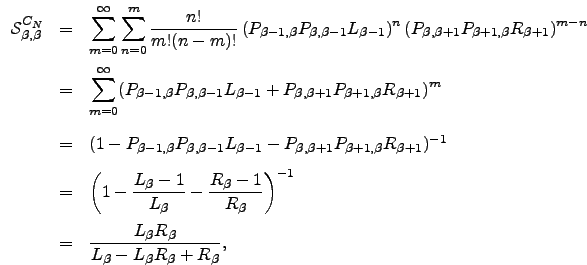 we can write
we can write