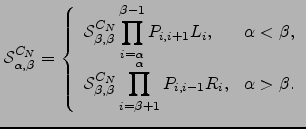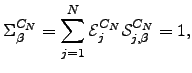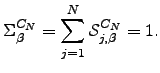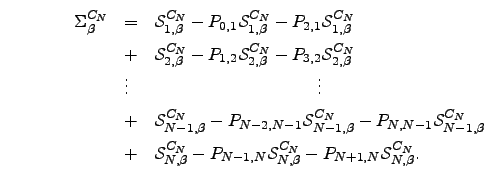
Next: FINDING THE SHORTEST AND Up: thesis Previous: PATHWAY SUMS FOR CHAIN Contents

TOTAL ESCAPE PROBABILITY FOR CHAIN GRAPHS, #MATH971#

So long as there is at least one escape route from 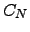the total escape probability must be unity:

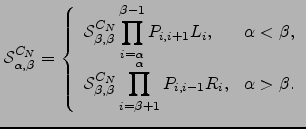$\displaystyle \Sigma_{\beta}^{C_N} = \sum_{j=1}^{N} \mathcal{E}_{j}^{C_N} \mathcal{S}_{j,\beta}^{C_N} = 1,$

(D.1)

otherwise, if is the empty set, we have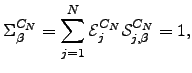

$\displaystyle \Sigma_{\beta}^{C_N} = \sum_{j=1}^{N} \mathcal{S}_{j,\beta}^{C_N} = 1.$

(D.2)

For example, to show that the formulae in Appendix C are consistent with the first result we expand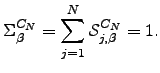

$\displaystyle \mathcal{E}_{j}^{C_N} = 1-P_{j-1,j}-P_{j+1,j}$

(D.3)

and define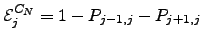

$\displaystyle P_{0,1}=P_{N+1,N}=0$

(D.4)

for convenience, so that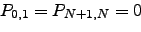

$\begin{displaymath}\begin{array}{lll} \Sigma_{\beta}^{C_N} &=& \mathcal{S}^{C_N}... ...}_{N,\beta} - P_{N+1,N}\mathcal{S}^{C_N}_{N,\beta}. \end{array}\end{displaymath}$

(D.5)

Using the recursion relations in Equation C.2 (which assume that there is an escape route from 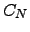) we can show that

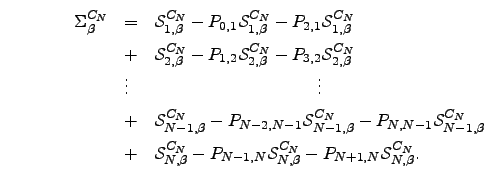$\displaystyle \mathcal{S}^{C_N}_{j,\beta}-\mathcal{S}^{C_N}_{j-1,\beta} P_{j,j-1}-\mathcal{S}^{C_N}_{j+1,\beta} P_{j,j+1} =0,$

(D.6)

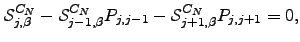for $j\not=\beta$ . We can now group together terms in Equation D.5 into sets of three that sum to zero. The terms that do not immediately cancel are as follows. From the first and second lines of Equation D.5 we have

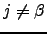$\displaystyle \mathcal{S}^{C_N}_{1,\beta}- P_{2,1}\mathcal{S}^{C_N}_{2,\beta}=0$

(D.7)

because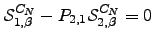

$\displaystyle \mathcal{S}^{C_N}_{1,\beta}=\mathcal{S}^{C_N}_{2,\beta}P_{2,1}L_1=\mathcal{S}^{C_N}_{2,\beta}P_{2,1}.$

(D.8)

Similarly, on the last two lines we find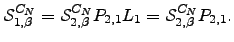

$\displaystyle \mathcal{S}^{C_N}_{N,\beta}-P_{N,N-1}\mathcal{S}^{C_N}_{N-1,\beta}=0$

(D.9)

because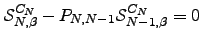

$\displaystyle \mathcal{S}^{C_N}_{N,\beta}=P_{N,N-1}\mathcal{S}^{C_N}_{N-1,\beta}R_N= P_{N,N-1}\mathcal{S}^{C_N}_{N-1,\beta}.$

(D.10)

The final remaining terms are: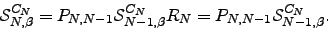

$\begin{displaymath}\begin{array}{rll} && \mathcal{S}^{C_N}_{\beta,\beta} -\mathc... ...L_\beta R_\beta}{L_\beta R_\beta} \right) \\ &=& 1, \end{array}\end{displaymath}$

(D.11)

which proves Equation D.1.

Next: FINDING THE SHORTEST AND Up: thesis Previous: PATHWAY SUMS FOR CHAIN Contents

Semen A Trygubenko 2006-04-10