Next: Creating a Coarse-grained Model Up: INTRODUCTION Previous: INTRODUCTION Contents

The Force Field

A general force field can be written as a series of terms representing the interactions between increasingly large sets of atoms [34,35]:

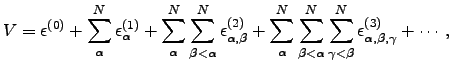$\displaystyle V = \epsilon^{(0)} + \sum_\alpha^N \epsilon^{(1)}_\alpha + \sum_\... ...alpha}^N \sum_{\gamma < \beta}^N \epsilon^{(3)}_{\alpha,\beta,\gamma} + \cdots,$

(3.1)

where 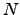is the total number of atoms, and the two-body term 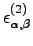$\epsilon^{(2)}_{\alpha,\beta}$ , for instance, describes the interaction of two atoms 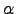$\alpha$ and $\beta$ .

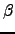Three-body and higher order terms in Equation 1.1 are often neglected, such as, for example, in the Lennard-Jones (LJ) pair potential [36,9], which takes the form

$\displaystyle V = 4 \epsilon \sum_{\beta<\alpha}^N \left[ \left(\dfrac{\sigma}{... ...beta}}\right)^{12} - \left(\dfrac{\sigma}{r_{\alpha,\beta}}\right)^{6} \right],$

(3.2)

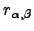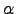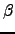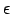where $r_{\alpha,\beta}$ is the distance between atoms $\alpha$ and $\beta$ , $\epsilon$ is the depth of the potential energy well, and 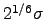$2^{1/6}\sigma$ is the pair equilibrium separation. This is an approximate potential as its form is a trade-off between the accurate reproduction of the interaction between closed-shell atoms and mathematical and computational simplicity. In this thesis we will use it to describe atomic clusters of various sizes.

Next: Creating a Coarse-grained Model Up: INTRODUCTION Previous: INTRODUCTION Contents

Semen A Trygubenko 2006-04-10