A Rotamers in the CHARMM19 Force Field

Appendix A
Rotamers in the CHARMM19 Force Field

The people may be made to follow a path of action,
but they may not be made to understand it.

Confucius (551 BC - 479 BC)

V (r_{1} (j), r_{2} (j), r_{3} (j), \dots, r_{N} (j))

is the energy functional that describes a system with

N

atoms,

where

r_{i} (j)

the three-dimensional vector that contains the Cartesian coordinates of atom

i

for

structure

j

i.e.

r_{i} (j) = (X_{i} (j), Y_{i} (j), Z_{i} (j))

, where

X_{i} (j)

is the

X

coordinate of

atom

i

in structure

j

, etc. Structure

A

is fully specified by

a set of coordinates

{r_{1} (A), r_{2} (A), r_{3} (A), . . . r_{N} (A)}

Ideally, the energy functional is invariant with respect to any permutations

within a subset of atoms of the same element. For example, if atoms

1

and

2

are

both hydrogens, swapping their coordinates around should not make any

difference for the evaluation of energy and its derivatives. This effectively

means that ‘numbering’ or ‘labelling’ of the atoms within such a subset is

completely arbitrary. Swapping the coordinates and relabelling are

therefore equivalent operations.

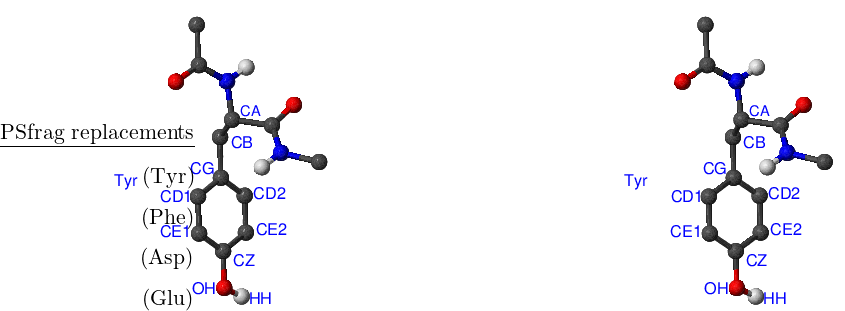
The CHARMM19 energy functional [4] is capable of describing some of the permutational isomers. While it is not possible to swap two atoms of the same type that belong to different residues (a rearrangement of this type would involve bond breaking and is thus impossible to model with CHARMM), rotations of the side chains can map an initial structure onto a permutational isomer. Such rotational isomers (rotamers) can be thought of as structures where symmetry-related atoms are relabelled. For example, in the phenylalanine side chain a rotation around a bond CB–CG by 180 degrees generates a structure that could otherwise be obtained via permutation CD1 $\Leftrightarrow$ CD2 followed by CE1 $\Leftrightarrow$ CE2 [see Figure A.1(Phe)]. CB, CG, CD1 etc. are CHARMM19 atom types as specified in CHARMM19 topology and parameter files, toph19.inp and param19.inp.

Figure A.1:Amino acids that have ring- and carboxylic-based rotameric sidechains. Stereo ball-and-stick models of CHARMM19 representations of phenylalanine, tyrosine, aspartic and glutamatic acids are shown. For the description of the atom colour-coding see the caption to Figure 2.10. Each molecule was optimised using CHARMM19, and has standard Ace and Cbx capping groups blocking N- and C-termini, respectively. Atoms involved in the definition of asymmetric torsions are labelled with their respective CHARMM19 atom names.

Landscape searching using the DPS method [8, 10] involves precise identification of the stationary points, which is best done by comparing their energies and the principal components of the inertia tensor. Recently Evans and Wales applied DPS to met-enkephalin and the B1 domain of protein G [133, 197, 290]. They noted that permutational isomers of stationary points using the CHARMM19 force field can have slightly different energies and geometries even if tightly optimised.^∗

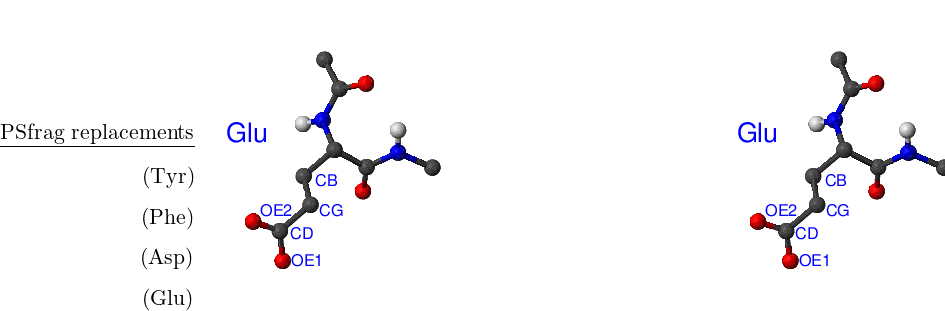
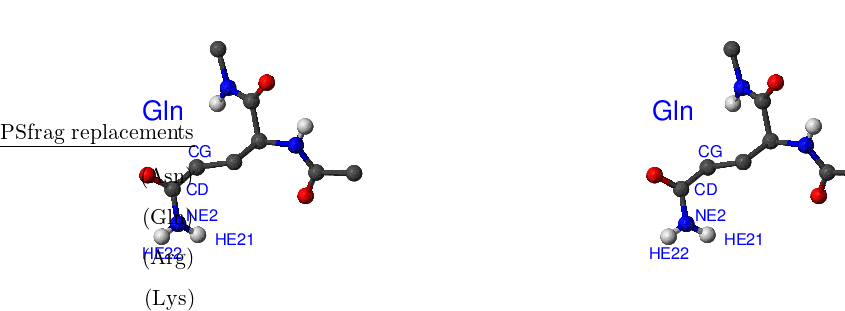
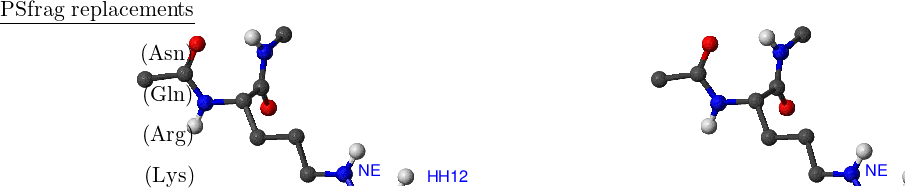
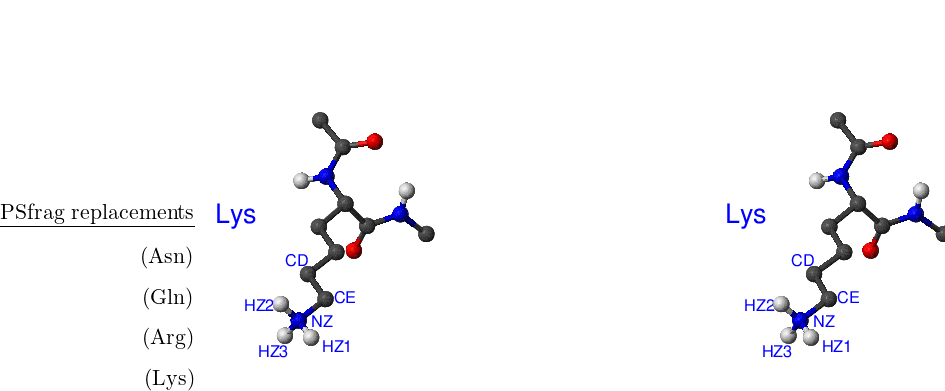
There are eight amino acids that have side chain rotamers in CHARMM19. The aromatic rings in tyrosine and phenylalanine have two pairs of carbon-hydrogen united atoms in the ring that are equivalent, namely, CD1, CD2 and CE1, CE2. Aspartic and glutamic acids each have a pair of equivalent oxygens — OD1, OD2 and OE1, OE2, respectively. Ball-and-stick models of Phe, Tyr, Asp and Glu amino acids are shown in Figure A.1. Asparagine, glutamine and arginine have equivalent hydrogens in amino groups. Lysine has three equivalent hydrogens in the NH $_{3}^{+}$ – group. Asn, Gln, Arg and Lys amino acids are depicted in Figure A.2.

Figure A.2:Amino acids that have isomers due to rotation of –NH $_{2}$ and –NH $_{3}^{+}$ groups. Stereo ball-and-stick models of CHARMM19 representations of asparagine, glutamine, arginine and lysine are shown. For the description of the atom colour-coding see the caption to Figure 2.10. Each molecule was optimised using CHARMM19, and has standard Ace and Cbx capping groups blocking N- and C-termini, respectively. Atoms involved in the definition of asymmetric torsions are labelled with their respective CHARMM19 atom names.

Standard CHARMM19 N- and C-terminal capping groups ‘Nter’ and ‘Cter’ also have rotational isomers. Finally, methyl groups in valine and leucine side chains can be swapped without bond breaking. Cter, Nter, Val and Leu are shown in Figure A.3.

Figure A.3:Amino acids that have isomers that are related by an operation of methyl group swapping. Stereo ball-and-stick models of CHARMM19 representations of valine and leucine are shown. For the description of the atom colour-coding see the caption to Figure 2.10. Each molecule was optimised using CHARMM19, and has standard Nter and Cter capping groups blocking N- and C-termini, respectively. Atoms involved in the definition of asymmetric torsions are labelled with their respective CHARMM19 atom names.

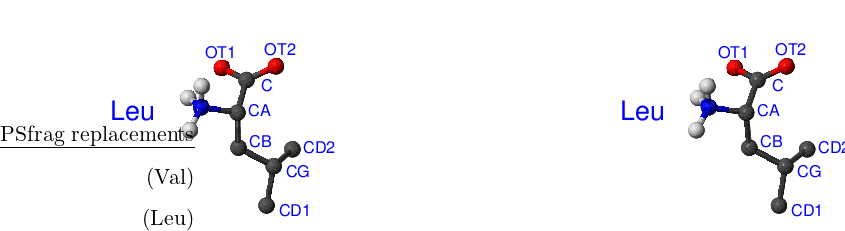
Rotamers of tyrosine, asparagine, glutamine and the C-terminal residue Cter can have different energies in the CHARMM19 force field. The energy difference can be as large as $1 0^{- 3}$ kcal/mol for tightly optimised structures and is due to the asymmetry in the definition of the dihedral angle in the case of tyrosine, asparagine and glutamine, and in the definition of the improper dihedral angle in the case of Cter.

It is easy to demonstrate this effect for tyrosine with a structure for which the axis of rotation of the phenyl ring (which passes through atoms CG and CZ) does not coincide with the torsion axis (which passes through atoms CZ and OH). In this case the angles of the torsion CE1–CZ–OH–HH in the two rotamers are not complementary, which results in a slightly different energy. A similar situation is found in asparagine and glutamine where rotation of aminogroups is described by asymmetric CB–CG–ND2–HD21 and CG–CD–NE2–HE21 dihedral angles, respectively.

The same asymmetry is present in another tyrosine torsion, CA–CB–CG–CD1, as well as the CA–CB–CG–CD1 torsion in phenylalanine, the CB–CG–CD–OE1 torsion in glutamic acid, and the CA–CB–CG–OD1 torsion in aspartic acid, but they are not noticeable when a standard parameter file is used because the corresponding force constants are zero.

The improper torsion C–CA–OT2–OT1 is the origin of the energy difference for the Cter residue [see Figure A.1(Leu)]. In the general case it is difficult to symmetrise improper torsions in CHARMM19 without changing the form of the energy functional and/or reparametrisation. Fortunately, when the equilibrium angle is zero the improper torsion term is a symmetric function of the angle and, provided symmetry-related atoms are given in ‘correct’ order, the improper torsion energy and its derivatives will be the same in both rotamers. Specifically, for improper torsion I–J–K–L, where I is the central atom and the torsion angle is the angle between the plane defined by atoms I–J–K and atom L, if the symmetry related atoms are J and K then $ϕ$ (I–J–K–L)= $- ϕ$ (I–K–J–L). While tyrosine improper torsions CG–CD1–CD2–CB and CZ–CE1–CE2–OH, phenylalanine CG–CD1–CD2–CB improper torsion, the CD–OE1–OE2–CG improper torsion for glutamic acid, and the CG–OD1–OD2–CB improper torsion for aspartic acid are all symmetrically specified, the Cter’s C–CA–OT2–OT1 improper torsion is not.

The valine and leucine situation is special because if one of the two structures with side chains that are mirror images of one another is a stationary point the other one is not. In other words, because the rearrangement where the –C–C(CH $_{3}$ ) $_{2}$ group undergoes an inversion is not describable by the force field, only one of the two isomers can exist on the CHARMM19 potential energy surface as a stationary point.

We have fixed the dihedral asymmetries in Asn, Gln, Tyr, Phe, Glu, Asp, Val and Leu by adding multiple dihedral terms between bonds with similar symmetry-related positions and halving the corresponding force constants, as was advised by Prof. Charles L. Brooks III. We also ‘symmetrised’ the Cter improper torsion by changing the topology for that residue. Patches for toph19.inp, param19.inp, toph19_eef1.inp and param19_eef1.inp are available online [165].

[prev] [prev-tail] [front] [up]

Appendix ARotamers in the CHARMM19 Force Field

Appendix A
Rotamers in the CHARMM19 Force Field